Vavilonski brojevi
| Brojevni sistemi po kulturama | |
|---|---|
| Hindu-Arapski brojevi | |
| Zapadnoarapski Indijska familija Kmerski |
Istočnoarapski Brami Tajski |
| Istočnoazijski brojevi | |
| Kineski Sučou |
Računski štapići Mongolski |
| Alfabetski brojevi | |
| Abžadski Jermenski Ćirilični Ge'ez |
Hebrejski Grčki (Jonski) Āryabhaṭa |
| Ostali sistemi | |
| Atički Vavilonski Egipatski Inuitski |
Etrurski Majanski Rimski Polje urni |
| Spisak tema o brojevnim sistemima | |
| Pozicioni sistemi po bazama | |
| Dekadni (10) | |
| 2, 4, 8, 16, 32, 64 | |
| 1, 3, 6, 9, 12, 20, 24, 30, 36, 60, još… | |
Vavilonski brojevi ili Babilonski brojevi su deo sistema za predstavljanje numeričkih vrednosti u staroj Vaviloniji. Takođe su bili deo klinastog pisma, tj. ispisivani su trščanom pisaljkom s vrhom u obliku klina, kojim se ostavljao trag na mekanoj glinenoj tablici, koja bi zatim bila ostavljena na Suncu da se stvrdne i ostavi trajan zapis.
Vavilonci su poznati po svojim astronomskim/astrološkim promatranjima i proračunima (v. Vavilonska astronomija) pri čemu su koristili abakus i seksagezimalni (sa osnovom 60) pozicioni sistem, nasleđen od sumerske i akadske civilizacije.
Sistem se prvi put pojavio oko 3100. pne., pa se smatra da je to bio prvi poznati brojevni sistem sa pozicionom notacijom, u kojem vrednost cifre zavisi i od njene pozicije unutar broja. Ovo je bilo otkriće od najvećeg značaja, jer sistemi bez te osobine zahtevaju posebne simbole za predstavljanje svakog stepena osnove (npr. 10, 100, 1000 itd., u decimalnom sistemu) što bi otežalo računanje.
Pretpostavlja se da je 60 izabrano za osnovu zbog svoje faktorizacije prostim brojevima (2×2×3×5) i deljivosti mnogim brojevima: svima od 1 do 6, kao i sa 10, 12, 15, 20 i 30.
Za predstavljanje 59 cifara različitih od nule su korišćena samo dva simbola:
- za brojanje jedinica -
(moguće i klin nadole, nalik slovu "V"[1]) - za brojanje desetica -
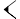
Ovi simboli i njihove vrednosti su kombinovane u cifru prema principu znakovne notacije, slično kao u rimskim brojevima. Npr. kombinacija 
je predstavljala cifru 23 (videti dole tabelu cifara). Za poziciju bez vrednosti je ostavljan prazan prostor, nalik današnjoj nuli/ništici. Vavilonci su kasnije iznašli znak za predstavljanje ovog praznog mesta. Nisu imali simbol za decimalni zarez, pa se o poziciji jedinica moralo zaključiti na osnovu konteksta: je moglo vredeti 23 ili 23×60 ili 23×(60×60) ili 23/60 itd.
Moguće i da su neke cifre mogle biti predstavljane drugačije, npr. 38 kao 40-2 ([1]).
Sistem je jasno koristio unutrašnje dekade za predstavljanje cifara, ali to nije bio zaista sistem mešovitog korena (radiksa), sa osnovama 10 i 60, jer je podosnova 10 korišćena samo da olakša predstavljanje velikog broja potrebnih cifara; pozicije u nizovima cifara su dosledno imale bazu 60, pa je i aritmetika potrebna rad sa tim nizovima cifara bila seksagezimalna.
Tragovi seksagezimala su ostali do danas u načinu na koji se izražavaju ugaoni stepeni: 360° u krugu, 60' (minuta) u stepenu, 60 (sekundi) u minuti; poslednje dve jedinice se ekvivalentno koriste i u računanju vremena.
Vavilonci, tehnički gledano, nisu imali cifru za ni koncept nule. Mada su razumeli ideju ništavila, to se nije smatralo za broj, već za nedostatak broja. Umesto toga, Vavilonci su imali prazan prostor (kasnije i simbol za popunjavanje pozicije) da označe nepostojanje cifre na određenoj poziciji.
(na engleskom:)
- Menninger, Karl W. (1969). Number Words and Number Symbols: A Cultural History of Numbers. MIT Press. ISBN 0-262-13040-8.
- McLeish, John (1991). Number: From Ancient Civilisations to the Computer. HarperCollins. ISBN 0-00-654484-3.
(na engleskom:)
- Babylonian numerals Arhivirano 2017-05-20 na Wayback Machine-u
- Cuneiform numbers Arhivirano 2004-06-03 na Wayback Machine-u
- Babylonian Mathematics
- High resolution photographs, descriptions, and analysis of the root(2) tablet (YBC 7289) from the Yale Babylonian Collection
- Photograph, illustration, and description of the root(2) tablet from the Yale Babylonian Collection Arhivirano 2012-08-13 na Wayback Machine-u
- Babylonian Numerals by Michael Schreiber, Wolfram Demonstrations Project.
- Weisstein, Eric W., "Sexagesimal", MathWorld.
