Elektrostatika

Naelektrisani kompakt-disk privlači komadiće papira

Elektrostatika je grana fizike koja se bavi pojavama i svojstvima stacionarnih ili sporokrećućih naelektrisanja koja nemaju ubrzanje.

Od antičkih vremena je poznato da određeni materijali kao što je ćilibar privlače lagane čestice nakon trljanja. Grčka reč za ćilibar (grč. ήλεκτρον electron), je koren reči elektricitet. Elektrostatičke pojave potiču od sile koja se javlja između naelektrisanja. Te sile su opisane Kulonovim zakonom. Iako elektrostatički indukovane sile izgledaju prilično slabe, elektrostatičke sile između elektrona i proton protona koji sačinjavaju atom vodonika su oko 36 puta jače od gravitacionih sila između njih.

Postoji mnoštvo primera za elektrostatičke pojave, od jednostavnih kao što je privlačenje plastične kuhinjske folije za vašu ruku nakon što je odmotate iz pakovanja, do naizgled spontanih eksplozija silosa sa žitom, do oštećenja elektronskih komponenti tokom proizvodnje i funkcionisanja fotokopir mašine. Elektrostatika je povezana sa nagomilavanjem naelektrisanja na površini objekata zbog dodira sa drugim površinama. Iako se razmena naelektrisanja dešava svaki put kada se neke dve površine dodirnu i odvoje, efekat razmene naelektrisanja se uglavnom jedino primeti kada bar jedna od površina ima veliki otpor prema kretanju naelektrisanja. To se dešava zato što naelektrisanja koja prelaze sa ili na visoko otpornu površinu su više ili manje zarobljena na njoj dovoljno dugo da bi efekti naelektrisanja mogli da se posmatraju. Ova naelektrisanja ostaju na objektu dok ne pređu ka zemlji ili se brzo neutrališu elektrostatičkim pražnjenjem. Poznati efekat elektrostatičkog udara nastaje neutralizacijom nakupljenog naelektrisanja u telu kontaktom sa neprovodnim površinama.

Kulonov zakon

Kulonov zakon za intenzitet elektrostatičke sile (u njutnima) između dva tačkasta naelektrisanja $q$ i $Q$ (u kulonima). Pogodno je označiti jedno od ovih naelektrisanja, $q$ , kao testno naelektrisanje, i nazvati $Q$ naelektrisanjem izvora. Kako se teorija bude proširivala, dodaće se još izvora naelektrisanja. Ako je $r$ udaljenost (u metrima) između dva naelektrisanja, onda je sila:

F={\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ}{r^{2}}}=k_{e}{\frac {qQ}{r^{2}}}\,,

gde je ε₀ propustljivost vakuuma^[1]

\varepsilon _{0}={10^{-9} \over 36\pi }\;\;\mathrm {C^{2}\ N^{-1}\ m^{-2}} \approx 8.854\ 187\ 817\times 10^{-12}\;\;\mathrm {C^{2}\ N^{-1}\ m^{-2}} .

Internacionalne SI jedinice ε₀ su ekvivalentne A²s⁴ kg⁻¹m⁻³ or C²N⁻¹m⁻² or F m⁻¹. Kulonova konstanta je:

k_{e}\approx {\frac {1}{4\pi \varepsilon _{0}}}\approx 8.987\ 551\ 787\times 10^{9}\;\;\mathrm {N\ m^{2}\ C} ^{-2}.

Korišćenje ε₀ umesto k₀ u izražavanju Kulonovog zakona je povezano sa činjenicom da je sila inverzno proporcionalna površini lopte sa poluprečnikom jednakim udaljenosti između dva naelektrisanja.

Jedan proton ima naelektrisanje e, a jedan elektron ima naelektrisanje −e, gde je,

e\approx 1.602\ 176\ 565\times 10^{-19}\;\;\mathrm {C} .

Ove fizička konstanta fizičke konstante (ε₀, k₀, e) su trenutno definisane tako da ε₀ i k₀ su egzaktno definisane, a e je mera količine.

Električno polje

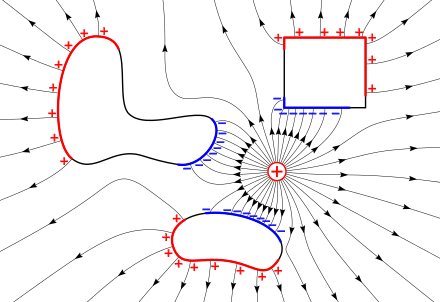
Linije električnog polja su pogodne za vizuelno predstavljanje električnog polja. Linije polja imaju početak na pozitivnom naelektrisanju i imaju kraj na negativnom naelektrisanju u bilo kojoj tački. Električno polje, ${\vec {E}}$ , (u jedinicama volti po metru) je vektorsko polje koje može da se definiše bilo gde, osim na mestu gde se nalaze tačkasta naelektrisanja (gde teži beskonačnosti). Pogodno je postaviti hipotetičko testno naelektrisanje u tački gde se ne nalaze druga naelektrisanja. Po Kulonovom zakonu, ovo testno naelektrisanje će osetiti silu koja može da se iskoristi za definisanje električnog polja na sledeći način:

{\vec {F}}=q{\vec {E}}.\,

(Pogledati Lorencove jednačine ukoliko naelektrisanje nije stacionarno)

Razmotriti skup ${\vec {E}}$ čestica naelektrisanja $Q_{i}$ , koja se nalaze u tačkama ${\vec {r}}_{i}$ , električno polje u ${\vec {r}}$ (zvano tačka polja) je:

{\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\frac {{\hat {\mathfrak {r}}}_{i}Q_{i}}{\left\|{\mathfrak {\vec {r}}}_{i}\right\|^{2}}},

gde je ${\vec {\mathfrak {r}}}_{i}={\vec {r}}-{\vec {r}}_{i},$ je vektor premeštanja od tačke polja izvora ${\vec {r}}_{i}$ do tačke polja ${\vec {r}}$ , i ${\hat {\mathfrak {r}}}_{i}={\vec {\mathfrak {r}}}_{i}/\left\|{\vec {\mathfrak {r}}}_{i}\right\|$ je jedinični vektor koji pokazuje smer polja. Za tačkasto naelektrisanje koje se nalazi u koordinatnom početku, intenzitet ovog električnog polja je $E=k_{e}Q/r^{2},$ i usmeren je od tog naelektrisanja. Činjenica da se sila (a samim tim i polje) može izračunati sabiranjem svih vrednosti individualnih čestica koje su izvori naelektrisanja je primer principa superpozicije. Električno polje koje nastaje od naelektrisanja je zadato u [[gustina naelektrisanja|gustini naelektrisanja u zapremini $\rho ({\vec {r}})$ i može biti izračunato konvertujući ovu sumu u trostruki integral:

{\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}}}\iiint {\frac {{\vec {r}}-{\vec {r}}\,'}{\left\|{\vec {r}}-{\vec {r}}\,'\right\|^{3}}}\rho ({\vec {r}}\,')\operatorname {d} ^{3}r\,'

Gausov zakon

Gausov zakon kaže da "ukupan električni fluks kroz bilo koju zatvorenu hipotetičku površinu bilo kog oblika unutar električnog polja, proporcionalan ukupnom naelektrisanju unutar te površine“. Matematički, Gausov zakon ima oblik integralne jednačine:

\oint _{S}{\vec {E}}\cdot \mathrm {d} {\vec {A}}={\frac {1}{\varepsilon _{0}}}\,Q_{enclosed}=\int _{V}{\rho  \over \varepsilon _{0}}\cdot \operatorname {d} ^{3}r,

gde je $\operatorname {d} ^{3}r=\mathrm {d} x\ \mathrm {d} y\ \mathrm {d} z$ element zapremine. Ako je naelektrisanje raspoređeno po površini ili duž linije, zameniti $\rho \mathrm {d} ^{3}r$ sa $\sigma \mathrm {d} A$ ili $\lambda \mathrm {d} \ell$ . Teorema Divergencije dozvoljava da se Gausov zakon napiše u diferencijalnom obliku:

{\vec {\nabla }}\cdot {\vec {E}}={\rho  \over \varepsilon _{0}}.

gde je ${\vec {\nabla }}\cdot$ operator divergencije.

Poasonove i Laplasove jednačine

Definicija elektrostatičkog potencijala, kombinovana sa diferencijalnim oblikom Gausovog zakona (iznad), daje relaciju između potencijala Φ i gustine naelektrisanja ρ:

{\nabla }^{2}\phi =-{\rho  \over \varepsilon _{0}}.

Ova relacija je oblik Poasonove jednačine. U odsustvu neuparenih naelektrisanja, jednačina postaje Laplasova jednačina:

{\nabla }^{2}\phi =0,

Elektrostatička aproksimacija

Ispravnost elektrostatičke aproksimacije se oslanja na pretpostavku da je električno polje ne rotirajuće:

{\vec {\nabla }}\times {\vec {E}}=0.

Iz Faradejevog zakona indukcije, ova pretpostavka podrazumeva odsustvo ili skoro potpuno odsustvo vremenski promenljivih magnetnih polja:

{\partial {\vec {B}} \over \partial t}=0.

Drugim rečima, elektrostatika ne zahteva odsustvo magnetnih polja ili električnih struja. Tačnije, ukoliko magnetna polja postoje ili električne struje, one ne smeju da se menjaju tokom vremena, ili u najgorem slučaju, moraju da se menjaju u toku vremena veoma polako. U nekim problemima, i elektrostatika i magnetostatika su potrebni za dobijanje tačnih prognoza, ali međusobni efekti mogu i dalje da se ignorišu.

Elektrostatički potencijal

Pošto je električno polje ne rotirajuće, moguće je izraziti električno polje kao gradaciju skalarne funkcije, $\phi$ , koja se naziva elektrostatičkim potencijalom ili poznatije naponom. Električno polje, $E$ , je usmereno od oblasti sa visokim električnim potencijalom ka oblastima sa malim električnim potencijalom, matematički izraženo sa

{\vec {E}}=-{\vec {\nabla }}\phi .

Teorema gradijenta može da se iskoristi kako bi se ustanovilo da je elektrostatički potencijal mera fizičkog rada po jedinici naelektrisanja koje je potrebno da bi se naelektrisanje pomerilo iz tačke $a$ u tačku $b$ , izraženo integralom:

-\int _{a}^{b}{{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}}=\phi ({\vec {b}})-\phi ({\vec {a}}).

Iz ovih jednačina, vidimo da je električni potencijal konstantan u bilo kojoj oblasti u kojoj nema električnog polja (kao što se dešava unutar provodnih objekata).

Elektrostatička energija

Potencijalna energija jedne testne čestice, $U_{\mathrm {E} }^{\text{single}}$ , može da se izračuna iz integrala uloženog rada, $q_{n}{\vec {E}}\cdot \mathrm {d} {\vec {\ell }}$ . Integracija se vrši iz tačke koja je beskonačno udaljena, i pretpostavlja se da se skup $N$ čestica sa naelektrisanjem $Q_{n}$ , već nalazi u tačkama ${\vec {r}}_{i}$ . Ova potencijalna energija (u DŽulima) je:

U_{\mathrm {E} }^{\text{single}}=q\phi ({\vec {r}})={\frac {q}{4\pi \varepsilon _{0}}}\sum _{i=1}^{N}{\frac {Q_{i}}{\left\|{\mathfrak {\vec {r}}}_{i}\right\|}}

gde je ${\vec {\mathfrak {r}}}_{i}={\vec {r}}-{\vec {r}}_{i},$ razdaljina svakog naelektrisanja $Q_{i}$ od testnog naelektrisanja $q$ , koje se nalazi u tački ${\vec {r}}$ , a $\phi ({\vec {r}})$ je električni potencijal koji bi se nalazio ${\vec {r}}$ da testno naelektrisanje nije prisutno. Ako su prisutna samo dva naelektrisanja, potencijalna energija jednaka je $k_{e}Q_{1}Q_{2}/r$ . Ukupna električna potencijalna energija koja nastaje od prisustva skupa od N naelektrisanja se izračunava sabiranjem potencijalnih energija svake čestice:

U_{\mathrm {E} }^{\text{total}}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{j=1}^{N}Q_{j}\sum _{i=1}^{j-1}{\frac {Q_{i}}{r_{ij}}}={\frac {1}{2}}\sum _{i=1}^{N}Q_{i}\phi _{i},

gde suma, j = 1 do N, isključuje i = j:

\phi _{i}={\frac {1}{4\pi \varepsilon _{0}}}\sum _{j=1(j\neq i)}^{N}{\frac {Q_{j}}{4\pi \varepsilon _{0}r_{ij}}}.

Ovaj električni potencijal, $\phi _{i}$ je vrednost koja bi se izmerila u tački ${\vec {r}}_{i}$ ako bi nedostajalo naelektrisanje $Q_{i}$ . Ova formula očigledno isključuje beskonačno veliku energiju koja bi bila potrebna za sakupljanje svake tačke naelektrisanja iz oblaka naelektrisanja. Suma naelektrisanja može da se konvertuje u integral nad gustinom naelektrisanja koristeći sledeći recept $\sum (\cdots )\rightarrow \int (\cdots )\rho \mathrm {d} ^{3}r$ :

U_{\mathrm {E} }^{\text{total}}={\frac {1}{2}}\int \rho ({\vec {r}})\phi ({\vec {r}})\operatorname {d} ^{3}r={\frac {\varepsilon _{0}}{2}}\int \left|{\mathbf {E} }\right|^{2}\operatorname {d} ^{3}r

,

Ovaj drugi izraz za elektrostatičku energiju koristi činjenicu da je električno polje negativna gradacija električnog potencijala. Ova dva integrala za električno polje naizgled pokazuju dve međusobno isključujuće formule za gustinu elektrostatičke energije, tj. ${\frac {1}{2}}\rho \phi$ i ${\frac {\varepsilon _{0}}{2}}E^{2}$ ; one dobijaju iste vrednosti za ukupnu elektrostatičku energiju, samo ako se izvrši integracija obe jednačine kroz ceo prostor.

Elektrostatički pritisak

Na električnom provodniku, površinska naelektrisanja će osećati silu u prisustvu električnog polja. Ova sila je usrednjena vrednost diskontinualnog električnog polja na površinsko naelektrisanje. Ova usrednjena vrednost u odnosu na polje prisutno odmah oko površine daje:

P={\frac {\varepsilon _{0}}{2}}E^{2}

,

Ovaj pritisak ima tendenciju da uvlači provodnik u polje, nezavisno od znaka površinskog naelektrisanja.

Triboelektrična serija

Triboelektrični efekat je vrsta elektrifikacije kontakta u kojoj određeni materijal postaje naelektrisan kada dodirne drugi kontakt od drugog materijala, pa se zatim udalji od njega. Jedan od materijala dobija pozitivno naelektrisanje, a drugi jednako negativno naelektrisanje. Znak i jačina naelektrisanja koji nastaju se razlikuje od vrste materijala, površinske gruboće, temperature, opterećenja, i drugih osobina. Ćilibar na primer može da primi naelektrisanje trljanjem sa materijalom kao što je vuna. Ovu osobinu je prvi put zabeležio Tales iz Mileta, i predstavlja prvi električni fenomen koji je čovek istražio. Drugi primeri materijala koji mogu da dobiju značajno naelektrisanje trljanjem su staklo koje se trlja o svilu, i tvrda guma koja se trlja o krzno.

Elektrostatički generatori

Prisustvo disbalansa površinskih naelektrisanja znači da će tela pokazati privlačne ili odbojne sile. Ovaj disbalans površinskih naelektrisanja koji dovodi do statičkog elektriciteta, može da nastane dodirivanjem dve različite površine i njihovim odvajanjem zbog fenomena elektrifikacije kontakata i triboelektričnog efekta. Trljanje dva neprovodna tela stvara veliku količinu statičkog naelektrisanja. Ono nije samo rezultat trenja; dve neprovodne površine mogu da se naelektrišu samo postavljanjem jedne na drugu. Pošto većina površina ima grubu površinu, potrebno je da prođe više vremena za naelektrisanje kontaktom nego trljanjem. Trljanje objekata međusobno povećava veličinu kontaktne površine između njih. Uglavnom izolatori, supstance koje ne provode elektricitet, su dobre za generisanje i zadržavanje površinskog naelektrisanja. Neki primeri ovakvih materijala su guma, plastika i staklo. Provodnici se retko naelektrišu sem u slučajevima kada je npr. metalna površina udarena čvrstim ili tečnim izolatorom. Naelektrisanje koje se prebacuje preko elektrifikacije kontakta se čuva na površinama objekata. Elektrostatički generatori su uređaji koji proizvode veoma veliki napon sa veoma malom strujom i koriste se u učionicama za demonstraciju fizike a njihov princip rada se oslanja na prethodno opisan efekat.

Primetite da prisustvo električnih struja ne utiče na smanjenje elektrostatičkih sila ili varničenja.

Neutralizacija naelektrisanja

Prirodni elektrostatički fenomeni su poznati kao povremeno dosadne pojave u sezonama male vlažnosti vazduha, ali mogu biti destruktivni u nekim situacijama (npr. u proizvodnji elektronike). Kada se radi u direktnom kontaktu sa integrisanim elektronskim komponentama (posebno osetljivim MOSFET tranzistorima), ili u prisustvu zapaljivog gasa, moraju se preduzeti mere opreza da bi se sprečilo skupljanje i naglo elektrostatičko pražnjenje.

Indukcija naelektrisanja

Indukcija naelektrisanja se javlja kada negativno naelektrisano telo odbija elektrone sa površine drugog tela. Ovo stvara oblast u drugom telu koje je više pozitivno naelektrisano. Privlačna sila se onda javlja između dva objekta. Npr. kada se balon trlja, balon će se zalepiti za zid jer je privlačna sila javlja između dve suprotno naelektrisane površine (zid dobija električno naelektrisanje zbog indukcije naelektrisanja, pošto se slobodni elektroni na površini zida odbijaju o negativno naelektrisan balon, stvarajući pozitivno naelektrisanu površinu zida, koja se zbog toga privlači sa površinom balona). Istražite ovaj efekat pomoću simulacije balloon and static electricity.

Statički elektricitet

Pre 1832. godine kada je Majkl Faradej objavio rezultate svog eksperimenta na temu identiteta elektriciteta, fizičari su "statički elektricitet" smatrali drugačijim u odnosu na ostala naelektrisanja. Majkl Faradej je dokazao da su elektricitet indukovan magnetom, naponski elektricitet iz baterije i statički elektricitet jednaki.

Statički elektricitet uobičajeno nastaje kada se dva materijala trljaju jedan o drugi, kao vuna na plastici ili đon cipela po tepihu. Proces čini da se elektroni izvuku iz površine jednog materijala i premeste na površinu drugog materijala.

Elektrostatički udar nastaje kada površina drugog materijala, negativno naelektrisana elektronima, dodirne pozitivno naelektrisan provodnik, ili suprotno.

Statički elektricitet se koristi u kserografiji, filterima vazduha i nekim automobilskim bojama. Statički elektricitet je nakupljeno naelektrisanje na dva tela koji su postali odvojeni jedno od drugog. Male elektronske komponente mogu lako da se oštete statičkim elektricitetom. Proizvođači komponenata koriste razne antistatičke uređaje da ovo izbegnu.

Statički elektricitet i hemijska industrija

Kada se različiti materijali spoje i odvoje, može da se akumulira naelektrisanje koje ostavlja jedan materijal pozitivno a drugi negativno naelektrisanim. Mali udar koji osetite kada pipnete uzemljeni predmet nakon hodanja po tepihu je primer viška naelektrisanja koje se akumuliralo u vašem telu od trenja između vaših cipela i tepiha. Rezultujuće naelektrisanje vašeg tela može da izazove jako električno pražnjenje. Iako eksperimentisanje sa statičkim elektricitetom može biti zabavno, slične varnice mogu da dovedu do velikih opasnosti u industrijama koje se bave zapaljivim materijalima, gde mala električna varnica može da zapali eksplozivnu smešu sa velikim posledicama.

Sličan način naelektrisanja nastaje kada tečnosti male provodljivosti struje teku duž cevi - proces koji se zove elektrifikacija mlaza. Tečnosti koje imaju malu električnu provodljivost (ispod 50 pikosimensa po metru, gde je pikosimens po metru mera električne provodljivosti), nazivaju se akumulatori. Tečnosti koje imaju provodljivost iznad 50 pikosimensa po metru se nazivaju ne-akumulatori. Kod ne-akumulatora, naelektrisanja se brzo rekombinuju dok se razdvajaju i zato naelektrisanje koje nastaje nije značajno. U petrohemijskoj industriji, 50 pikosimensa po metru je minimalna vrednost električne provodljivosti za adekvatno uklanjanje naelektrisanja iz tečnosti.

Značajan koncept za izolovanje tečnosti je vreme statičke relaksacije. Ovo je slično vremenskoj konstantni (tau) unutar RC kola. Za izolacioni materijal, ovo predstavlja odnos statičke dielektrične konstante podeljen sa električnom provodljivošću materijala. Za ugljovodonične tečnosti, ova mera se ponekad aproksimira deljenjem broja 18 sa električnom provodljivošću tečnosti. Tako tečnost koja ima električnu provodljivost od 1 pS/cm (100 pS/m) će imati procenjenu vrednost vremena relaksacije od oko 18 sekundi. Višak naelektrisanja u tečnosti će biti skoro kompletno odstranjen nakon 4 do 5 vremena relaksacije, ili 90 sekundi za primer iznad.

Proizvodnja naelektrisanja se povećava sa većim brzinama tečnosti i većim prečnicima cevi, postajući vrlo značajna u cevima prečnika 200mm ili većim. Britanski standard BS PD CLC/TR 50404:2003 (ranije BS-5958-Part 2) Ponašanje pri kontroli neželjenih statičkih naelektrisanja propisuje maksimalne brzine protoka. Zbog velikog značaja na dielektričnu konstantu, preporučena vrednost za ugljovodonične tečnosti koje sadrže vodu je ograničen na 1 m/s.

Uzemljavanje je uobičajen način za sprečavanje sakupljanja naelektrisanja. Za tečnosti koje imaju električnu provodljivost ispod 10 pS/m uzemljavanje nije dovoljno za disipaciju naelektrisanja, već je potrebno dodati anti-statičke aditive.

Standardi

1.BS PD CLC/TR 50404:2003 Code of Practice for Control of Undesirable Static Electricity

2.NFPA 77 (2007) Recommended Practice on Static Electricity

3.API RP 2003 (1998) Protection Against Ignitions Arising Out of Static, Lightning, and Stray Currents

Elektrostatička indukcija u komercijalnoj primeni

Princip elektrostatičke indukcije je korišćen mnogo godina u industriji, počev od elektrostatičkih industrijskih sistema za farbanje automobila, bicikala i drugih proizvoda.

Povezano

Elektromagnetizam

Reference

↑ Matthew Sadiku (2009). Elements of electromagnetics. str. 104. ISBN 9780195387759.

Literatura

Matthew Sadiku (2009). Elements of electromagnetics. str. 104. ISBN 9780195387759.
Faraday, Michael (1839). Experimental Researches in Electricity. London: Royal Inst. Besplatna e-knjiga: e-book na Projektu Gutenberg
Halliday, David; Robert Resnick; Kenneth S. Krane (1992). Physics. New York: John Wiley & Sons. ISBN 0-471-80457-6.
Griffiths, David J. (1999). Introduction to Electrodynamics. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-805326-X.
Hermann A. Haus and James R. Melcher (1989). Electromagnetic Fields and Energy. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-249020-X.
William J. Beaty, "Humans and sparks; The Cause, Stopping the Pain, and 'Electric People". 1997.
William Cecil Dampier, "The theory of experimental electricity". Cambridge [Eng.] University press, 1905 (Cambridge physical series). xi, 334 p. illus., diagrs. 23 cm. LCCN 05040419 //r33
William Thomson Kelvin, Reprint of Papers on Electrostatics and Magnetism By William Thomson Kelvin, Macmillan 1872
Alexander MacAulay Utility of Quaternions in Physics. Electrostatics—General Problem. Macmillan 1893
Alexander Russell, A Treatise on the Theory of Alternating Currents. Electrostatics. University Press 1904

Spoljašnje veze

Man's static jacket sparks alert". BBC News, 16 September 2005.
"Can shocks from static electricity damage your health? Arhivirano 2009-07-05 na Wayback Machine-u". Wolfson Electrostatics News pages.
Invisible wall of static
Downloadable electrostatic BEM modules in MATLAB for simple capacitance problems Arhivirano 2016-03-04 na Wayback Machine-u
Introduction to Electrostatics: Point charges can be treated as a distribution using the Dirac delta function

[Sadiku-1] Matthew Sadiku (2009). Elements of electromagnetics. str. 104. ISBN 9780195387759.

[1]