Pravilni poliedri

„Kocke“ u obliku pravilnih poliedara. Koriste se za dobijanje slučajnih brojeva u određenom opsegu

Pravilni poliedri (ili platonska čvrsta tela) su pravilni konveksni poliedri čije su zajedničke karakteristike:

• Svaki pravilni poliedar je omeđen površima istog oblika
• Ove površi su pravilni mnogoulgovi,
• Iz svakog temena jednog pravilnog poliedra polazi jednak broj ivica,
• Jedan pravilni poliedar se ne može dobiti spajanjem više drugih

Ovih geometrijskih tela ima svega pet:

1. tetraedar,
2. heksaedar (kocka),
3. oktaedar,
4. dodekaedar i
5. ikosaedar.

Površina poliedra

Površina geometrijskog tijela je ukupna površina svih ploha koje ga omeđuju. Površina poliedra je zbir površina svih njegovih strana.

Prizma

B – površina baze

P – površina strane,

o –obim baze

v – dužina visine

$P==2B+P$

Za uspravnu prizmu vrijedi

$P=2B+ov.$

Piramida

B – površina baze

P – površina strane

v – dužina visine

$P=B+P$

Krnja piramida

$B_{1}$, $B_{2}$ – povrsine baza

P – površina strana

v – dužina visine

$P=B_{1}+B_{2}+P$

Zapremina

Zapremina geometrijskog tijela je mjera prostora kojeg tijelo zauzima.

Prizma

$V=Bv$

Piramida

$V={\frac {1}{3}}Bv$

Krnja piramida

$V={\frac {v}{3}}(B_{1}+B_{2}+{\sqrt {B_{1}B_{2}}})$

Pet pravilnih poliedara

Pet pravilnih poliedara
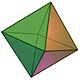
Ime	Tetraedar	Heksaedar ili Kocka	Oktaedar	Dodekaedar	Ikosaedar
Slika	(Animacija)	(Animacija)	(Animacija)	(Animacija)	(Animacija)
Razmotana figura
Površi	4 trougla	6 kvadrata	8 trouglova	12 petouglova	20 trouglova
Broj ivica/temena	6 / 4	12 / 8	12 / 6	30 / 20	30 / 12
Broj ivica u jednom temenu	3	3	4	3	5

Kocka

Kocka je pravilna četverostrana prizma. Spada u paralelepipede. Sastoji se od šest podudarnih kvadrata, njenih strana. Ima 12 ivica i 8 vrhova.

Formule

Zapremina $V=a^{3}$

Površina $P=6a^{2}$

Manja dijagonala $d=a{\sqrt {2}}$

Prostorna dijagonala $D=a{\sqrt {3}}$

Radijus upisane sfere $r_{u}={\frac {a}{2}}$

Radijus opisane sfere $r_{o}={\frac {{\sqrt {3}}a}{2}}$

Oktaedar

Oktaedar je geometrijsko tijelo omeđeno sa osam međusobno podudarnih površi koje imaju oblik jednakostranicnih trouglova i raspoređene su tako da tijelo ima dvanaest ivica i sest tjemena.

Oktaedar se još može opisati i kao jednakostranična četvrostrana bipiramida i kao jednakostranična linearna antiprizma.

Formule

Zapremina $V={\frac {\sqrt {2}}{3}}a^{3}$

Površina $P=2{\sqrt {3}}a^{2}$</math>

Poluprečnik upisane sfere $r_{u}={\frac {\sqrt {6}}{6}}a$

Poluprečnik opisane sfere $r_{o}={\frac {\sqrt {2}}{2}}a$

Ikosaedar

Ikosaedar je omeđen sa dvadeset međusobno podudarnih površi koje imaju oblik jednakostraničnih trouglova. Raspoređene su tako da tijelo ima trideset ivica i dvanaest tjemena.

Formule

1. Površina $P=5{\sqrt {3}}a^{2}$
2. Zapremina$V={\frac {5}{12}}\left(3+{\sqrt {5}}\right)a^{3}$
3. Poluprečnik upisane sfere $r_{u}={\frac {a}{12}}{\sqrt {3}}\left(3+{\sqrt {5}}\right)$
4. Poluprečnik upisane sfere$r_{o}={\frac {a}{4}}{\sqrt {10+2{\sqrt {5}}}}$

Dodekaedar

Dodekaedar je geometrijsko tijelo omeđeno sa dvanest međusobno podudarnih površi koje imaju oblik

Formule

Površina $P=3{\sqrt {25+10{\sqrt {5}}}}\,a^{2}$

Zapremina $V={\frac {1}{4}}\left(15+7{\sqrt {5}}\right)a^{3}$

Poluprečnik upisane sfere |$r_{u}={\frac {\sqrt {5}}{20}}{\sqrt {50+22{\sqrt {5}}}}\,a$

Poluprečnik opisane sfere $r_{o}={\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\,a$

Tetraedar

Tetraedar je geometrijsko tijelo koga ograničavaju četiri trougaone površi i, koje zajedno sa dijelom prostora koga omeđuju jednoznačno formiraju tijelo sa četiri tjemena i šest ivica.

Naziv se u koristi za pravilni tetraedar, kod koga su ove četiri površi podudarni jednakostranični trouglovi.

Formule

Površina $P={\sqrt {3}}a^{2}$

Zapremina $V={\begin{matrix}{1 \over 12}\end{matrix}}{\sqrt {2}}a^{3}$

Poluprečnik opisane sfere $r_{o}\,=\,{\frac {\sqrt {6}}{4}}\,a\approx 0{,}61\,a$

Poluprečnik upisane sfere $r_{u}\,=\,{\frac {\sqrt {6}}{12}}\,a\approx 0{,}20\,a$

Visina $h=r_{o}+r_{u}\,=\,{\frac {\sqrt {6}}{3}}\,a\,=\,{\sqrt {\frac {2}{3}}}\,a\approx 0{,}82\,a$

Ugao između ivice i površi $arctg{\sqrt {2}}\approx 55^{\circ }$

Ugao između dvije površi $\arccos {1/3}=arctg2{\sqrt {2}}\approx 71^{\circ }$

Pravilni poliedri na Wikimedijinoj ostavi