Lagranževa tačka

Lagranžove tačke (L-tačke) je naziv za pet tačaka u orbitalnoj konfiguraciji gde malo telo na koje deluje samo gravitacija može da bude nepokretno u odnosu na dva veća tela (npr. veštački satelit u odnosu na Zemlju i Mesec). U Lagranžovim tačkama gravitaciona dejstva dva veća tela poništavaju centrifugalnu silu koja bi izbacila telo iz orbite. Ove tačke su analogne geostacionarnim orbitama u smislu da se uzajamni položaji tela u sistemu ne menjaju vremenom.
Preciznija definicija kaže da su Lagranžove tačke stacionarna rešenja redukovanog problema tri tela.[1][2]
Istorija i koncept[uredi | uredi kod]
Tri kolinearne Lagranžove tačke je prvi otkrio Ojler oko 1750. godine.[3]
Italijansko-francuski matematičar Žozef Luj Lagranž je 1772. radio na čuvenom problemu tri tela, kada je otkrio zanimljivu posledicu svojih rezultata. Lagranž je pokušao da pronađe jednostavan način za računanje gravitacionih interakcija proizvoljnog broja tela, jer prema Njutnovoj mehanici tela se u takvom sistemu kreću haotično dok ne dođe do sudara ili neka tela budu izbačena iz sistema tako da se ostatak sistema nađe u ravnoteži. Problem jednog tela je trivijalan, jer je ono statično u odnosu na samo sebe, problem dva tela je jednostavan jer se oba tela kreću oko zajedničkog centra mase; međutim uvođenjem dodatnih tela se matematičke jednačine drastično komplikuju. Potrebno je izračunati uticaj svih tela na sva druga tela na svakoj tački njihove putanje.
Lagranž je želeo da pojednostavi problem. Uveo je jednostavnu hipotezu: Putanja objekta je određena putem koji minimizuje akciju tokom vremena. Takvu putanju je moguće naći oduzimanjem potencijalne od kinetičke energije. Ovakvim razmišljanjem, Lagranž je reformulisao klasičnu Njutnovu mehaniku i došao do tzv. Lagranžove mehanike. Dalji rad je doveo Lagranža do hipoteze kako će se telo zanemarljive mase kretati oko dva tela koja se već nalaze na približno kružnim orbitama. U referentnom sistemu koji rotira zajedno sa većim telima, Lagranž je našao 5 specifičnih tačaka u kojima se poništavaju sile koje deluju na malo telo[4]. U njegovu čast su ove tačke nazvane „Lagranžove tačke“. Tek posle sto godina (1990-ih) su otkriveni Trojanski asteroidi, čije orbite se nalaze u Lagranžovim tačkama sistema Sunce-Jupiter.
U opštijem slučaju eliptičnih orbita, ne postoje više stacionarne „tačke“, već se javljaju Lagranžove „oblasti“. Lagranžove tačke konstruisane za svaku konfiguraciju sistema grade elipse matematički slične elipsama koje opisuju veća tela, što je posledica drugog Njutnovog zakona. Telo u Lagranžovoj tački ima isti orbitalni period kao i dva veća tela, i ovaj orbitalni period ne zavisi od oblika putanje, što znači da su eliptične putanje koje opisuju Lagranžove tačke zapravo rešenja jednačine kretanja za treće telo.
Lagranžove tačke[uredi | uredi kod]
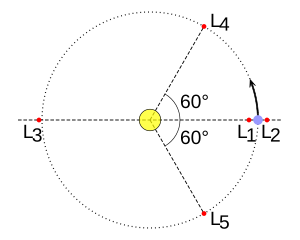
Pet lagranžovih tačaka nosi sledeće oznake:
L1[uredi | uredi kod]
L1 tačka leži na liniji koja spaja veće mase M1 and M2, i to između ovih tela. Ovu je tačku intuitivno najlakše razumeti, u njoj gravitacija manjeg se direktno suprotstavlja gravitaciji većeg tela.
- Primer: Telo koje kruži oko Sunca bliže od Zemlje bi trebalo da ima kraći orbitalni period, ali time zanemarujemo efekt Zemljine gravitacije. Ako se objekt nalazi na liniji koja spaja Zemlju i Sunce, Zemljina gravitacija deluje nasuprot Sunčeve, povećavajući pri tom orbitalni period objekta. Što je objekt bliže Zemlji, i efekt je veći. U L1 tački, orbitalni period objekta i Zemlje postaju jednaki.
L1 tačka u sistemu Sunce-Zemlja je idealna za posmatranje Sunca. Solarna i heliosferna opservatorija (SOHO) je smeštena u Halo orbiti oko L1, a satelit Napredni istraživač sastava (ACE) u Lisažu orbiti, takođe oko L1. Zemlja-Mesec L1 omogućava lak pristup orbitama i oko Zemlje i oko Meseca uz minimalnu promenu brzine zbog čega je idealna za svemirsku stanicu koja bi prenosila ljude i teret do Meseca i nazad.
L2[uredi | uredi kod]

L2 tačka leži na pravoj definisanoj većim masama, iza manjeg tela. U ovom slučaju se gravitaciona dejstva oba tela suprotstavljaju centrifugalnoj sili trećeg tela.
- Primer: Sa one strane Zemlje suprotne Suncu, orbitalni period bi normalno bio duži od orbitalnog perioda Zemlje. Dodatno gravitaciono privlačenje Zemlje skraćuje taj orbitalni period koji u L2 postaje jednak periodu revolucije Zemlje.
L2 tačka u sistemu Sunce-Zemlja je dobra pozicija za svemirska posmatranja. Kako objekti u L2 zadržavaju istu orijentaciju u odnosu na Zemlju i Sunce, kalibracija i zaštita su značajno jednostavniji. Vilkinsonova stanica za mikrotalasnu anizotropiju (engl. Wilkinson Microwave Anisotropy Probe) se već nalazi u orbiti oko L2, a u planu su i Plankov satelit, Heršel svemirska opservatorija, Gaja stanica i Džejms Veb svemirski teleskop. L2 tačka u sistemu Zemlja-Mesec predstavlja pogodnu tačku za postavljanje komunikacionih satelita za dalju stranu Meseca.
Ako je masa manjeg tela (M2) mnogo manja od mase većeg objekta (M1), onda se L1 i L2 nalaze na približno istoj udaljenosti r od manjeg tela, jednakoj poluprečniku Hilove sfere:
gde je R udaljenost između M1 i M2.
Primeri:
L3[uredi | uredi kod]
L3 tačka leži kolinearno sa većim telima, iza većeg od njih
- Primer: L3 u sistemu Sunce-Zemlja se nalazi na suprotnoj strani Sunca u odnosu na Zemlju, malo bližu Suncu nego Zemlja, jer se centar mase u sistemu Sunce-Zemlja ne nalazi u sentru Sunca već nešto bliže Zemlji. Kao i u L2, i u L3 tački zajedničko gravitaciono privlačenje Sunca i Zemlje dovodi do toga da tela imaju isti period revolucije kao Zemlja.
U petparačkoj naučnoj fantastici i stripovima L3 je bila populatno mesto za smeštanje „anti-Zemlje“, ali kada se jednom započelo sa lansiranjem svemirskih sondi, pokazano je da takvo telo ne postoji, Štaviše, Sunce-Zemlja L3 tačka je izuzetno nestabilna zbog gravitacionog dejstva drugih planeta. Venera, na primer, svakih 20 meseci prolazi na manje od 0,3 AJ od L3.
L4 i L5[uredi | uredi kod]

L4 i L5 tačke leže na temenima jednakostraničnog trougla čija je osnova definisana većim telima. Tačka L4 se nalazi ispred, a L5 iza manjeg tela gledano u odnosu na njegovu revoluciju oko većeg. Obe ove Lagranžove tačke leže u ravni orbite manjeg tela.
Ove dve tačke su stabilne jer su jednako udaljene od obe mase, pa je sila kojom veća tela na njih deluju proporcionalna masama M1 i M2, tako da rezultanta sile prolazi kroz centar mase. U L4 i L5 ne mora da se nalazi telo zanemarljive mase u odnosu na M1 i M2; opštu trougaonu konfiguraciju je otkrio Lagranž proučavajući problem 3 tela.
L4 i L5 se ponekad nazivaju trougaone Lagranžove tačke ili Trojanske tačke. Naziv Trojanske tačke potiče od trojanskih asteroida, koji se nalaze u L4 i L5 tačkama sistema Sunce-Jupiter. Asteroidi u L4 su nazvani „grčki tabor“ a u L5 „trojanski tabor“, i nose imena odgovarajućih junaka Ilijade.
- Primeri:
- Sunce-Zemlja L4 i L5 tačke sadrže međuplanetarnu prašinu
- u Sunce-Jupiter L4 i L5 tačkama se nalaze trojanski asteroidi
- u L4 i L5 tačkama sistema Sunce-Neptun se nalaze tela iz Kajperovog pojasa.
- Saturnov satelit Tetida ima dva manja satelita u svojim L4 i L5 tačkama – Telesto i Kalipso (respektivno)
- Saturnov satelit Dionu prate sateliti Helena i Polideuk u L4 i L5 tačkama (respektivno)
- prema hipotezi gigantskog sudara planeta veličine Mars po imenu Teja je postojala u Zemljinoj L4 ili L5 tački, ali je zbog svoje veličine postala nestabilna, sudarila se sa Zemljom, a kao posledica sudara je nastao Mesec.
Stabilnost[uredi | uredi kod]
Prve tri Lagranžove tačke su stabilne samo u ravni normalnoj na pravu definisanu dvama telima. Ovo je najočiglednije kod L1. Na probnu masu pomerenu normalno u odnosu na duž koja spaja M1 i M2 delovaće privlačna sila oba tela koja teži da telo vrati u ravnotežnu tačku. Ovo se dešava jer se komponente sile normalne na M1-M2 duž superponiraju, dok su komponentne paralelne sa ovom duži uravnotežene. Međutim, ako se probno telo pomeri bliže nekoj od masa, to telo će delovati jačom silom nego telo od koga je probna masa odmaknuta. (Ovakvo ponašanje je slično ponašanju pod dejtstvom plimskih sila).
Mada se može reći da su L1, L2 i L3 generalno nestabilne tačke, moguće je pronaći stabilne periodične orbite oko ovih tačaka, makar u restihovanom problemu tri tela. Ove potpuno periodilne orbite, koje se zovu „halo“ orbite, ne postoje u punom dinamičkom sistemu n-tela tako što je Sunčev sistem. U ovom slučaju postoje kvaziperiodične orbite koje prate Lisažuove krive, i ovakve Lisažuove orbite su koristile sve dosadašnje misije u Lagranžovim tačkama. Mada Lisažuove orbite nisu savršeno stabilne, potrebne su relativno skromne korekcije za održavanje letelica na željenim orbitama. U slučaju Sunce-Zemlja L1 tačke, pokazalo se korisnim da se svemirske misije smeste u Lasažuove orbite sa velikom amplitudom (100 000 – 200 000km), čime se smanjuje uticaj Sunčevog zračenja na komunikaciju Zemlje sa misijom.
Nasuprot kolinearnim Lagranžovim tačkama, trougaone tačke (L4 i L5) su tačke stabilne ravnoteže, pod uslovom da je odnos između -M1 i M2 veći od 24,96[5][6]. Ovo je slučaj za Suncem i Zemljom, dok je odnos Zemlje i Meseca za nijansu manji. Kada se telo pomeri iz trougaone Lagranžove tačke, Koriolisova sila ga zadržava na stabilmoj, bubrežastoj orbiti oko Lagranžove tačke (posmatrano iz rotirajućeg referentnog sistema). U sistemu Zemlja-Mesec, međutim, problem stabilnost je komplikovaniji zbog značajnog uticaja Sunčeve gravitacije [7]
Misije u Lagranžovim tačkama[uredi | uredi kod]
Zbog svoje specifičnosti, Lagranžove tačke su česta meta za neke vrste misija. Najčešće se misije nalaze u orbiti oko Lagranžovih tačaka, a ne u samim tačkama.
| Misija | Lagranžova tačka | Agencija | Status |
|---|---|---|---|
| Napredni istraživač sastava (engl. Advanced Composition Explorer, ACE) | Zemlja-Sunce L1 | NASA | Operativan |
| Solarna i heliosferska opservatorija | Zemlja-Sunce L1 | NASA | Operativan |
| Vetar (NASA) (globalni geosvemirski satelit) | Zemlja-Sunce L1 | NASA | Operativan |
| Postanje | Zemlja-Sunce L1 | NASA | Misija završena, napustila L1 tačku |
| Međunarodni istraživač kometa (engl. International Sun/Earth Explorer 3 (ISEE-3) | Zemlja-Sunce L1 | NASA | Originalna misija završena, napustila L1 tačku |
| Klimatska opservatorija dubokog svemira | Zemlja-Sunce L1 | NASA | Na čekanju |
| Solar-C | Zemlja-Sunce L1 | Japanska agencija za svemirska istraživanja | Misija moguća posle 2010. |
| Vilkinsonova sonda za mikrotalasnu anizotropiju | Zemlja-Sunce L2 | NASA | Operativan |
| Plankov satelit | Zemlja-Sunce L2 | ESA | Lansiranje planirano za proleće 2009. |
| Heršelova svemirska opservatorija | Zemlja-Sunce L2 | ESA | Lansiranje planirano za proleće 2009. (zajedno sa Plankovim Satelitom) |
| Džejms Veb svemirski teleskop | Zemlja-Sunce L2 | NASA, ESA, Kanadska svemirska agencija | Lansiranje planirano za jun 2013. ili kasnije |
| SMART-1 (Mala misija za napredna tehnološka istraživanja) | Mesec-Zemlja L1 (prolet) | ESA | Misija završena, namerno srušena na Mesec |
| Sunčeva senka | Zemlja-Sunce L2 | - | Različiti predlozi |
| Novi horizonti | Sunce-Neptun L5 (prolet) | NASA | Lansiran, planirano da stigne 1. avgusta 2014 |
Vidi još[uredi | uredi kod]
- Ojlerov problem tri tela
- Spisak tela u Lagranžovim tačkama
- Mesečev svemirski lift
- Potkovičasta orbita
- Hilova sfera
Izvori[uredi | uredi kod]
- ↑ "Redukovani problem tri tela", Science World.
- ↑ "Lagranžove tačke" Enrique Zeleny, Wolfram Demonstrations Project.
- ↑ Koon, W. S.; M. W. Lo, J. E. Marsden, and S. D. Ross (2006). Dynamical Systems, the Three-Body Problem, and Space Mission Design. str. 9.
- ↑ (fr) Lagrange, Joseph-Louis (1867-1892). „Tome 6, Chapitre II: Essai sur le problème des trois corps”. Oeuvres de Lagrange. Gauthier-Villars. str. 272–292.[mrtav link]
- ↑ Tačnije
- ↑ Lagranžove tačke – Nil Dž Korniš i Džeremi Gudman
- ↑ „Potraga za prirodnim ili veštačkim objektima smeštenim u Zemlja-Mesec libracionim tačkama”. Ikarus.
Eksterni linkovi[uredi | uredi kod]
- Objašnjenje Lagranžovih tačaka Arhivirano 2003-06-05 na Wayback Machine-u – Nil Dž Korniš (en)
- nasino objašnjenje – pripisano Nilu Dž Kornišu (en)
- Objašnjenje Lagranžovih tačaka – Džon Baez (en)
- Geometrija i proračuni Lagranžovih tačaka Arhivirano 2005-11-09 na Bibliotheca Alexandrina-u – Dž R Stokton (en)
- Mesta Lagranžovih tačaka, sa aproksimacijama – Dejvid Piter Stern (en)
- Mrežni kalkulator za računanje tačkog položaja svih 5 Lagranžovih tačaka u sistemu bilo koja 2 tela – Toni Dan (en)
![{\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1175643479ba922598c78a6d4dfcf7fff160bfe7)

