Rendgenska strukturna analiza

Rendgenska strukturna analiza (RSA) je tehnika za ispitivanje kristalnih supstanci, koja koristi difrakcionu sliku (difraktogram) dobijenu rasejavanjem rendgenskog zračenja (X-zračenja) na ispitivanom kristalu. Osnovni cilj RSA je određivanje kristalne i molekulske strukture (dužine veza između atoma, uglovi među vezama, apsolutne konformacije...) ispitivanog uzorka.
Rendgenskom strukturnom analizom moguće je odrediti strukturu velikog broja jedinjenja, koja se mogu naći u kristalnom obliku. Za složenija jedinjenja, kao što su različiti makromolekuli (DNK, proteini) potrebno je kombinovati ovako dobijene rezultate sa rezultatima dobijenim drugim analitičkim tehnikama, kao što je nuklearna magnetna rezonancija (NMR), i računarskim simulacijama da bi se dobila jasna slika o strukturi datih jedinjenja.
Kristalna struktura i mikrostruktura su u uskoj vezi s fizičkim i hemijskim svojstvima supstancije, pa je važnost rendgenske strukturne analize velika u nizu grana ljudske delatnosti. Utoliko je rentgenska strukturna analiza našla brojne primene u fizici i hemiji čvrstog stanja, hemiji, kristalohemiji, biohemiji, mineralogiji i biologiji, a izuzetnu primjenu ima u metalurgiji, keramičkoj, farmaceutskoj i uopšte hemijskoj industriji.
Istorijski podaci[uredi | uredi kod]
Rendgenski zraci otkriveni su 1895. godine, i ime su dobili prema svom pronalazaču, nemačkom naučniku Vilhelmu Konradu Rentgenu. Prve eksperimente sa difrakcijom X zračenja na kristalima sproveo je Maks fon Laue 1911. na kristalima soli. Odmah je uočen ogroman potencijal ove metode za određivanje strukture molekula — do tada dostupne samo preko hemijskih i hidrodinamičkih eksperimenata. Pioniri u razvoju rendgenske strukturne analize bili su i Vilijam Brag i Bernal. Prvi protein čija kristalna struktura je rešena bio je mioglobin jedne vrste kitova i to radovima Maksa Peruca i Džona Kendrjua (1958), za šta su dobili Nobelovu nagradu za hemiju.

Danas je primena RSA u strukturnoj biologiji veoma rasprostranjena — prema podacima Proteinske banke podataka (engl. Protein Data Bank ,PDB) od oko 42.000 proteina čija struktura je rešena, za oko 36.000 je zaslužna rendgenska strukturna analiza (NMR je doprinela sa oko 6.000 rešenih struktura, zatim slede elektronska mikroskopija, IC spektroskopija...).
Teorijske osnove[uredi | uredi kod]
Osnovni uslov koji treba ispuniti da bi došlo do difrakcije elektromagnetnog zračenja jeste da talasna dužina zračenja i dimenzije rešetke budu bliske. To je zadovoljeno jer je talasna dužina X-zračenja 10-9-10-11 m, što je istog reda veličine kao i razmak susednih ravni u kristalu (1-10 Ǻ).
Kada rendgenski zraci padnu na kristal atomi ili joni počinju da deluju kao novi, sekundarni izvori zračenja (Hajgensov princip), tj. dolazi do rasipanja rendgenskih zraka na elektronskim oblacima atoma. Između rasutih zraka dolazi do interakcije pri čemu se deo talasa pojačava, a deo slabi ili čak poništava i ta pojava poznata je kao difrakcija.
Postoje dva načina objašnjavanja fenomena difrakcije, Bragov zakon i Laueovi uslovi za difrakciju, kao i pristup preko recipročne rešetke (Evaldova sfera). Rezultati su ekvivalentni za različite pristupe.
Bragov zakon[uredi | uredi kod]
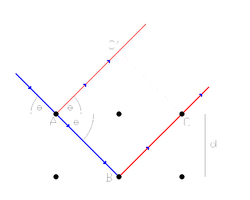
Prema Bragovom tumačenju, difrakcija je ekvivalentna refleksiji sa sistema paralelnih ravni u kristalu. Neka monohromatsko zračenje pada na kristal (slika ispod). Delom se reflektuje sa prve ravni, a delom sa druge.
Uslov za konstruktivnu interferenciju dva ovako dobijena zraka jeste da je njihova putna razlika jednaka celobrojnom umnošku talasnih dužina (λ) zračenja:
Iz ovog uslova i geometrijskih odnosa dobija se Bragov zakon:
gde je
- n – ceo broj, red difrakcije
- d – međuravansko rastojanje
- θ – ugao koji upadno zračenje zaklapa sa kristalom
Ovaj zakon nameće tačno određene uslove za θ i λ da bi došlo do difrakcije rendgenskih zraka. Različitim eksperimentalnim tehnikama ove dve veličine variraju se na različite načine i tako se stvaraju uslovi za pojavu difrakcije na kristalu. Intenziteti difrakcionih maksimuma zavise od vrste atoma u kristalnoj rešetki i od njihovog međusobnog prostornog rasporeda u skladu sa zahtevima simetrije, tj. zavise od kristalne strukture supstancije.
Evaldova sfera[uredi | uredi kod]
Evaldova sfera (sfera refleksije) je konstrukcija koja daje uslov za difrakciju u prostoru recipročne rešetke kristala. Svaka tačka recipročne rešetke odgovara jednoj ravni (hkl) realne rešetke, pa tako i mogućoj refleksiji sa te ravni. Talasni vektor upadnog i reflektovanog zračenja (kup i kref) su iste dužine, jer se zračenje rasejava elastično. Iz Bragovog zakona za recipročnu rešetku vidimo da je potreban i dovoljan uslov da do difrakcije zračenja dođe to da tačka recipročne rešetke leži na Evaldovoj sferi poluprečnika k (talasni broj zračenja koje se difraktuje). Eksperimentalno se to postiže rotiranjem ili oscilovanjem kristala, jer tada za isti ugao rotira ili osciluje i recipročna rešetka, pa će mnoge tačke recipročne rešetke proći kroz sferu refleksije i u tom trenutku pojaviće se difrakcioni maksimumi.
Kristalni uzorak je po definiciji periodične strukture; kristal je izgrađen ponavljanjem elementarne ćelije duž tri nezavisna pravca. Svaki difrakcioni pik odgovara refleksiji sa jedne ravni. Kako amplituda reflektovanog zračenja raste linearno sa brojem refleksija N sa iste vrste ravni opaženi intenzitet pikova raste sa N2. U periodičnim strukturama kao što je kristalna postoji ogroman broj paralelnih ravni (ekvivalentne u smislu difrakcije) što znatno pojačava zračenje dobijeno refleksijom i izdvaja ga iz šuma čineći ga merljivim. Zbog nepostojanja takve vrste uređenosti registrovan intenzitet kod amorfnih tela ili tečnosti je znatno manji. Još bitnije, u kristalu molekuli imaju tačno određenu orijentaciju zbog jakih međusobnih interakcija dok je u amorfnim telima ili tečnostima orijentacija molekula slučajna ili se menja sa vremenom pa je opaženi signal u stvari usrednjen signal po svim mogućim orijentacijama molekula u prostoru čime se automatski gubi bilo kakva informacija o strukturi.
Stoga su kristalne strukture neophodne za x-difrakciona ispitivanja, jer neuređena struktura vodi tome da u svim tačkama prostora dobijemo isti intenzitet rasutog zračenja, što nam ne daje nikakvu informaciju o datoj strukturi.
Eksperimentalne metode RSA-e[uredi | uredi kod]
Princip izvođenja RSA-e[uredi | uredi kod]

Na uzorak (monokristal ispitivanog jedinjenja) se usmerava snop x zračenja. U kristalografiji se koriste rendgenski zraci talasne dužine oko 1 Ǻ dobijeni pomoću rendgenske cevi. Većina metoda rendgenske strukturne analize zahteva da zračenje bude što bliže monohromatskom. U tu svrhu ispred ili iza uzorka na put rendgenskog zračenja se postavlja monohromator (kristal kvarca, grafita..) ili kod starijih instrumenata filtri od tanke metalne folije.
Menjanjem θ ili λ u zavisnosti od tehnike ostvaruju se uslovi za dobijanje difrakcione slike. Difrakcioni maksimumi se mogu detektovati, snimiti, pomoću proporcionalnog, scintilacionog brojača ili nekog drugog detektora ili na filmu. To je difrakciona slika uzorka, u kojoj su pohranjene sve informacije o strukturnim osobinama uzorka, o njegovoj kristalnoj strukturi i mikrostrukturi. Te osobine mogu se saznati indiciranjem difraktograma, tj. mjerenjem položaja difrakcionih maksimuma i analizom raspodele intenziteta duž difrakcione slike.
Savremeni uređaji za snimanje difrakcionih slika su automatski difraktometri za monokristale i polikristale sa odgovarajućom softver podrškom, i mogućnošću regulisanja uslova snimanja (temperatura, pritisak), slika 5.
Ako se odrede i intenziteti zračenja i fazne razlike u odnosu na upadno zračenje može se, Furijeovom transformacijom, kako je niže objašnjeno, odrediti prostorna distribucija elektronskih gustina:
- ρ (x,y,z)= ΣhΣkΣl Fo(h,k,l) exp(iΦhkl) exp(-2πi(hx+ky+lz))
Poznata hemijska struktura molekula koji sačinjava kristal omogućava da iz mape elektronske gustine dobijemo model kristala sa određenim položajem svakog atoma, funkcionalne grupe, strukture, u njemu.
Ispod je dat pregled metoda RSA-e i najznačajnije primene.
Klasifikacija eksperimentalnih metoda[uredi | uredi kod]
Zavisno od vrste uzorka i izbora eksperimentalne tehnike postoje različite metode rendgenske strukturne analize koje su prikazane u tabeli 1.
| Uzorak | Izvor rendgenskih zraka | Način beleženja rengenskih zraka | |
|---|---|---|---|
| Laueova | polihromatski | film | |
| Rotaciona i oscilatorna | monokristal | monohromatski | film |
| Vajsenbergova | monohromatski | film | |
| Precesiona | monohromatski | film | |
| Difraktometrija monokristala | monohromatski | detektor | |
| Debaj-Šererova | Prah | monohromatski | film (detektor) |
| Ginijeova | monohromatski | film | |
| Difraktometrija praha | monohromatski | detektor |
Metode kojima se ispituje polikristalni (praškasti) uzorak prvenstveno se koriste za identifikaciju prisutnih faza, tj. za kvalitativnu analizu uzorka. Ovim metodama mogu se odrediti i precizni parametri jedinične ćelije, stepen kristaliniteta uzorka, veličina kristalita i naponi u rešetki. Moguće je izvesti i kvantitativnu analizu, ili pratiti fazne transformacije. U novije vreme difraktometrija praha se dosta koristi i za određivanje kristalnih struktura jedinjenja sa višom simetrijom, pa čak i za rešavanje struktura svih tipva jedinjenja u tzv. ab initio postupcima. Metode kojima se ispituju monokristali primenjuju se za određivanje simetrije, prostorne grupe kristala i za izračunavanje parametara rešetke. Njihova najznačajnija primena je rečavanje kristalne strukture jedinjenja.
Određivanje strukture monokristala[uredi | uredi kod]
Velika primena RSA danas je, kao što je već pomenuto, u određivanju strukture proteina i drugih biomolekula. Ovde su opisani osnovni koraci u jednoj takvoj analizi proteina. Primenjuje se metod difrakcije na monokristalu, i kao što je gore pomenuto koristi se monohromatsko rendgensko zračenje. Koristi se monokristal ispitivanog jedinjenja.
Uslovi kristalizacije[uredi | uredi kod]
Stvaranje kristala dovoljno kvalitetnog za difrakciju (dovoljno pravilna struktura) je jedan od glavnih problema u eksperimentima određivanja atomske strukture proteina. Do sada je ovaj proces slabo razjašnjen i dobijanje dobrog kristala svodi se više na umetnost nego na nauku. Osnovna ideja je sporo, postepeno smanjenje rastvorljivosti molekula, bilo snižavanjem temperature ili povećavanjem koncentracije rastvora. Ako se proces izvede brzo ili sa neravnomernom promenom ovih veličina tj. uslova kristalizacije molekuli samo precipituju formirajući prah na dnu suda.
Proces kristalizacije sastoji se od dva stupnja: nukleacija (formiranje klice) i kristalni rast. Uslovi koji odgovaraju nukleaciji nisu uvek isti kao i oni koji pogoduju rastu kristala, a u svakom slučaju je teško pretpostaviti optimalne uslove za oba. Zato se praktično kristalizacija izvodi tako što se pripremi veliki broj rastvora ispitivanog molekula i zatim isprobavaju različiti uslovi- nije retko da se isprobaju stotine, čak i hiljade uslova da bi došlo do kristalizacije na odgovarajući način. U uslove koje variramo spadaju pH, različiti aditivi koji smanjuju rastvorljivost (različite soli Hofmaster serije), ili veliki polimeri (npr. polietilen glikol) koji izvlače molekule iz rastvora efektom entropije kao i različite početne temperature rastvora. Uvek se počinje sa vrlo koncentrovanim rastvorom, reda 40 mg/ml proteina.
Tradicionalne metode kristalizacije neorganskih jedinjenja modifikovane su u cilju primene na proteine, koji su termolabilni i osetljivi na visoke koncentracije organskih rastvarača. Koncentrovani rastvor proteina meša se sa različitim rastvorima koji se uglavnom sastoje od:
- Pufera, zbog kontrolisanja pH
- Precipitacioni agens, koji izaziva presićenost (obično polietilen glikoli, soli kao što su amonijum sulfat ili organski alkoholi)
- Druge soli ili aditivi, kao što su deterdženti ili kofaktori
Rastvor proteina se zatim koncentruje. Postoje mnoge metode kristalizacije koje rade na principu dijalize, difuzija tečnosti, mešanja dva rastvora kao i klasične metode isparavanja, kojima možemo dobiti kristale ispitivanih proteina. Pravilo je da se korisna informacija o strukturi može dobiti za kristale koji difraktuju sa rezolucijom većom od 4 angstrema (400pm), što je granica za kvalitet kristala koji želimo da dobijemo.
Poznati su neki faktori koji nepovoljno utiču na kontrolisanu kristalizaciju: vibracije ili bilo kakve nagle perturbacije, nečistoće. Takođe konformaciono fleksibilni delovi molekula inhibiraju kristalizaciju entropijskim efektima. Molekuli koji su prirodno asosovani (npr. fibrilarni proteini) generalno loše kristališu. Takođe i za kristalografiju je problem asosovanje ukoliko postoji i u kristalu, jer je generalno potreban monokristal. Do asosovanja molekula obično dolazi kod kristala kod kojih elementarna ćelija ima električni dipolni moment (feroelektrični kristali). U poslednje vreme napravljeni su neki pomaci u metodama izračunavanja koji omogućavaju određivanje i ovakvih struktura, mada je to još uvek teško.
Mnogi biomolekuli od interesa nisu još uvek kristalizovani na zadovoljavajući način. Nesavršenosti u strukturi kristala izazvane nečistoćama, ili postojanjem brojnih stabilnih konformacija proteina sprečavaju dobijanje slika atomske rezolucije. Čak je predloženo korišćenje Internacionalne svemirske stanice u procesu kristalizacije jer bestežinsko stanje redukuje uticaj varijacija u temperaturi na formiranje kristala.
Snimanje difraktograma[uredi | uredi kod]
Kada je formiran, kristal se postavlja tako da može da se nađe u snopu x zraka, i da je moguće rotirati ga. Ima više načina postavljanja uzorka. Jedan stariji je ubacivanje kristala u staklenu kapilaru napunjenu rastvorom iz kojeg je kristalisao, i postavljanje kapilare u difraktometar. Moderniji način je postavljanje kristala na tanku zakrivljenu žicu i fiksiranje mržnjenjem pomoću tečnog azota. Niska temperatura istovremeno redukuje oštećenja izazvanu na uzorku zbog velike energije dž zračenja, a i minimalizuje termalna kretanja koja na difroktogramu pojačavaju šum (Debaj-Velerov efekat). Problem je što može doći do pucanja kristala u struji tečnog azota pa je potrebna dodatna priprema uzorka, koja nije uvek izvodljiva.
Kristal se zatim postavlja u difraktometar koji je povezan sa izvorom x zračenja. To može biti ili rendgenska cev sa stacionarnom anodom (ulaz oko 2 kW JS), izvor tipa rotirajuće anode (ulaz oko 14 kW JS input) ili sinhroton (znatno jači fluks fotona). Pri odgovarajućim uslovima dolazi do difrakcije x zračenja, kako je gore objašnjeno, i difrakciona slika se snima na filmu ili u novije vreme beleži pogodnim detektorom i prenosi na računar. Sukcesivne slike dobijamo rotacijom kristala u snopu x zračenja.
Pre nego što je u eksperiment uvedeno hlađenje kristala podaci su dobijani na sobnim temperaturama. Zbog gore opisanih problema koji se javljaju pritom (šum) bilo je potrebno izvršiti mnogostruka merenja za jedan skup podataka što je produžavalo vreme analize. Danas je vreme analize dodatno smanjeno i korišćenjem skupa CCD detektora koji pokrivaju širok opseg uglova istovremeno.
Obrada podataka[uredi | uredi kod]
Osnovni cilj RSA-e jeste određivanje funkcije raspodele elektronske gustine, f(ρ) u kristalu. Podaci dobijeni eksperimentom predstavljaju reprezentaciju kristalne rešetke u recipročnom prostoru. Matematički je moguće iz toga dobiti izgled rešetke u realnom prostoru.
Furijeova transformacija[uredi | uredi kod]
Da bismo to uradili, eksperimentalno prikupljamo podatke o Furijeovoj transformaciji ove funkcije, F(q), koju zatim matematičkim putem obrađujemo da bismo dobili elektronsku gustinu u realnom prostoru. F(q) je strukturni faktor koji predstavlja relativni intenzitet rasutog zračenja duž pravca vektora difrakcije q, i izražava efekat relativne pozicije čestice na rasipanje. Strukturni faktor F(q) je u stvari Furijeova transformacija strukture. Važi:
a odgovarajuća formula Furijeove transformacije je:
što ćemo koristiti dalje.
Generalno, funkcija F(q) je kompleksna funkcija, tj. ima pored amplitude |F(q)|, i fazu Φ(q) :
Intenziteti difraktovanog zračenja dobijeni eksperimentalno su u korelaciji sa amplitudom |F(q)|. Korigovani intenzitet jednak je kvadratu amplitude. Korekcioni faktori su temperaturski, Lorenc-polarizacioni, faktor multipliciteta, i apsorpcioni faktor. Međutim intenzitet difraktovanog zračenja ni na koji način ne zavisi od faze Φ(q).
Može se pokazati da uvek važi:
tj. u opštem slučaju važi F(q) = F(-q), što je poznato kao Fridelov zakon (Friedel), a refleksije koje odgovaraju q tj. –q nazivaju se Fridelovi parovi. Kao posledica važenja Fridelovog zakona difrakciona slika dobijena sa bilo kog kristala uvek je centralno simetrična, što smanjuje broj eksperimentalnih podataka koje treba prikupiti pri rešavanju kristalne strukture.
Problem faze[uredi | uredi kod]
Postoji nekoliko načina da se odrede faze, tj. reši fazni problem. U najstarije metode za određivanje kristalne strukture spada metoda probe i greške. Ona se zasniva na tome da se pretpostavi model strukture, izračunaju strukturni faktori i uporede sa eksperimentalno dobijenim. Ova metoda može da se koristi za jednostavnije strukture i ima uglavnom istorijski značaj.
Danas postoji nekoliko pogodnih i široko korišćenih načina da se relativno brzo i jednostavno dođe do zadovoljavajućeg početnog modela. Neke metode se zasnivaju na izračunavanju približnih vrednosti Φ(q) iz poznatog položaja samo jednog ili nekoliko atoma (Patersonova funkcija, metoda teškog atoma, obično Hg), a druge pokušavaju da vrednosti Φ(q) odrede direktno (direktne metode). Za određivanje struktura kristala velikih organskih molekula, kao što su proteini i enzimi, uglavnom se koristi metoda izomorfne zamene, i metoda snimanja anomalija (MAD ,SAD).
Patersonova (Patterson) funkcija[uredi | uredi kod]
Vrlo poznata posledica Furijeove transformacije je autokorelaciona teorema koja kaže da je autokorelacija c(r) funkcije F(q)
Ima Furijeovu transformaciju C(q) koja je kvadrat amplitude funkcije F(q):
Stoga autokorelaciona funkcija C(q) elektronske gustine (tj. Patersonova funkcija) može biti izračunata direktno iz poznatih amplituda, bez poznavanja faze. U principu na ovaj način se može direktno odrediti kristalna struktura; međutim to je teško praktično realizovati. Autokorelaciona funkcija odgovara raspodeli vektora međuatomskog rastojanja u kristalu. Stoga Patersonova funkcija za kristal sa N atoma u elementarnoj ćeliji može imati N(N-1) maksimuma. S’ obzirom na neizbežne greške u merenju intenziteta i matematičkim problemima pri rekonstrukciji atomskih pozicija iz vektora međuatomskih polođaja i ova tehnika se koristi uglavnom za rešavanje strukture jednostavnijih kristala.
Model strukture[uredi | uredi kod]
Kada smo dobili podatak o početnoj fazi u stanju smo da formiramo početni model. Koordinate atoma i njihovi Debaj-Velerovi faktori se fituju prema eksperimentalnim podacima. Time dobijamo novi set faza i novu mapu elektronskih gustina. Zatim eksperimentator pregleda dobijene podatke, vrši korekcije na osnovu iskustva ili pretpostavki i počinje novi krug poboljšanja na isti način. To se nastavlja dok se ne postigne maksimalna korelacija između eksperimentalnih podataka i modela.
Kada je model molekulske strukture završen obično se unosi u neku kristalografsku bazu podataka, kao što je Proteinska Banka Podataka, Protein Data Bank (za proteine), ili Kembridž bazu podataka struktura, Cambridge Structure Database (za manje molekule). Mnoge strukture određene u privatnim, komercijalnim laboratorijama u medicinskim istraživanjima ne naleze se u javnim kristalografskim bazama podataka.
Prednosti i mane[uredi | uredi kod]
Nijedna druge tehnika otkrivena do sad ne nudi toliko podataka koliko RSA, tj. tačnije difrakcija na monokristalu. Tipičan kristal daje 20-30 hiljada refleksija, gde je svaka predstavlja jedan delić ukupne informacije o strukturi. Svi ovi podaci kompjuterskom obradom daju sliku raspodele elektronske gustine sa atomskom rezolucijom. Zahvaljujući tolikom broju nezavisnih podataka ovo i jeste najbolja metoda za određivanje atomske strukture bilo kog molekula.
Međutim, postoje i nedostaci, uglavnom povezani sa izvođenjem eksperimenta. Prvo, potreban je kristal zadovoljavajućeg kvaliteta, koji kao što smo videli nije lako dobiti. Neki kristalografi su posvetili i više od 10 godina svog života dobijanju monokristala proteina od interesa, npr. proteina gp120 koji virus HIV –a koristi da bi ušao u ljudsku ćeliju. Takođe bitan nedostatak je i to što na ovaj način ne dobijamo sliku molekula u svom prirodnom okruženju, što je bitno kod biomolekula. Dobijena struktura je prosečna struktura, a nemamo ni informaciju o recimo mobilnosti i pokretljivosti proteina.
Literatura[uredi | uredi kod]
- Lj. Karanović, D. Poleti, ‘Rendgenska strukturna analiza’, Zavod za udžbenike i nastavna sredstva, Beograd,2003
- Staff,’ Introduction to X-ray Diffraction’, Materials Research Laboratory, University of California, Santa Barbara.
- W.L. Bragg, "The Diffraction of Short Electromagnetic Waves by a Crystal", Proceedings of the Cambridge Philosophical Society, 17 (1912), 43–57.
- Ewald, P. P., editor ‘50 Years of X-Ray Diffraction’ (Reprinted in pdf format for the IUCr XVIII Congress, Glasgow, Scotland, Copyright © 1962, 1999 International Union of Crystallography).
- McPherson, A (1999). Crystallization of Biological Macromolecules. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. ISBN 0-87969-617-6.
- Drenth J. Principles of Protein X-Ray Crystallography. Springer-Verlag Inc. NY: 1999, ISBN 0-387-98587-5.
- Glusker JP, Lewis M, Rossi M. Crystal Structure Analysis for Chemists and Biologists. VCH Publishers. NY:1994, ISBN 0-471-18543-4.
- Rhodes G. Crystallography Made Crystal Clear. Academic Press. CA: 2000, ISBN 0-12-587072-8.
Spoljašnje veze[uredi | uredi kod]
- Kristalizacija malih molekula Arhivirano 2016-03-03 na Wayback Machine-u (en)








