Fraktal

Fraktali su geometrijski objekti čija je fraktalna dimenzija strogo veća od topološke dimenzije. Drugim riječima, to su objekti koji daju jednaku razinu detalja neovisno o razlučivosti koju koristimo. Dakle, fraktale je moguće uvećavati beskonačno mnogo, a da se pri svakom novom povećanju vide neki detalji koji prije povećanja nisu bili vidljivi, i da količina novih detalja uvijek bude otprilike jednaka. Oni su (barem približno) samoslični (sastoje se od umanjenih verzija samih sebe), ali isuviše nepravilni da bi se opisali jednostavnom geometrijom. Tako npr. dužina nije fraktal, iako je samoslična (sastoji se od beskonačno mnogo dužinâ, a sve su dužine slične). Laički rečeno, oni su "načičkani" do u beskonačnost.
Osnove[uredi | uredi kod]


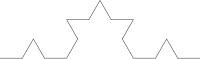

Kao jedan od najjednostavnijih i najpoznatijih primjera navest ćemo Kochovu krivulju. Ona se tvori tako da se dužina zamijeni likom prikazanim na prvoj slici lijevo. To se naziva prvom iteracijom Kochove krivulje. Druga se iteracija dobije tako da se svaka od četiri dužine iz prve iteracije zamijeni istim likom. Za treću iteraciju moramo zamijeniti svaku od 16 dužina itd. Kochovu krivulju dobijemo nakon beskonačnog broja iteracija. Na donjoj slici desno vidi se svojstvo samosličnosti - svaki je dio Kochove krivulje sličan cijeloj krivulji.
Još je jedan jednostavan primjer trokut Sierpińskog. Kreće se od trokuta (nulta iteracija) koji se zamijeni trima trokutima upola manje duljine stranice (prva iteracija). Sa svakim se trokutom postupak ponovi (druga iteracija), i tako u beskonačnost.

Fraktalna dimenzija[uredi | uredi kod]

Nakon velikog broja iteracija možemo vidjeti da duljina Kochove krivulje teži u beskonačnost kad broj iteracija teži u beskonačnost. No, cijela ta duljina je i dalje na istoj površini, samo je "zgužvana". Stupanj te "zgužvanosti" možemo vidjeti iz fraktalne dimenzije. Drugim riječima, ona nam daje uvid u to u kojoj mjeri neki fraktal zauzima ravninu (ili općenito n-dimenzionalni prostor u kojem se nalazi). Tako Kochova krivulja ima fraktalnu dimenziju približno 1.2619, a tepih Sierpińskog približno 1.8928. Iz vrijednosti, kao i iz slika, može se vidjeti da je tepih Sierpińskog "gušći", "načičkaniji" od Kochove krivulje, odnosno ispunjava veći dio ravnine.
Podjela[uredi | uredi kod]
Postoje razni načini klasifikacije fraktala. Jedan je od načina svrstati ih po stupnju samosličnosti. Potpuno samoslični fraktali su oni koji sadrže kopije sebe koje su slične cijelom fraktalu. Primjeri su svi geometrijski fraktali, npr. trokut Sierpińskog, Kochova krivulja, Hilbertova krivulja, Cantorov skup itd. Ako fraktal sadrži male kopije sebe koje nisu slične cijelom fraktalu, nego se pojavljuju u iskrivljenom obliku, govorimo o kvazi samosličnom fraktalu (Mandelbrotov i Julijin skup i sl.). Moguće je i da fraktal ne sadrži kopije samog sebe, ali da neke njegove osobine (npr. fraktalna dimenzija) ostaju iste pri različitim mjerilima. U tom slučaju govorimo o statističkoj samosličnosti, a tipičan je primjer Perlinov šum.
Fraktale je moguće klasificirati i po načinu njihova nastanka. Sustavi iteriranih funkcija (Iterated Function Systems – IFS) nastaju kopiranjem te homotetijom, rotiranjem i/ili translatiranjem kopije te mogućim zamjenjivanjem nekog elementa kopijom. Fraktali definirani rekurzivnim relacijama određeni su rekurzivnom matematičkom formulom koja određuje pripada li određena točka prostora (npr. kompleksne ravnine) skupu ili ne. Slučajni fraktali nastaju crtanjem grafova nekih stohastičnih procesa, npr. Brownovog gibanja. Zanimljivo je da i prva i druga podjela daje isti rezultat – sustavi iteriranih funkcija daju potpuno samoslične fraktale, fraktali definirani rekurzivnim relacijama su kvazi samoslični, a slučajni su fraktali samo statistički samoslični. Zbog jednostavnosti, za te ćemo tri skupine koristiti redom nazive geometrijski, algebarski i stohastični fraktali.
- geometrijski fraktali
- na pravcu
- u ravnini
- u trodimenzionalnom prostoru
- analogoni nižedimenzionalnim fraktalima
- Oktaedarski fraktal
- Dodekaedarski fraktal
- Ikosaedarski fraktal
- algebarski fraktali
- stohastični fraktali
Primjena[uredi | uredi kod]


Najjednostavniji primjer primjene fraktala u računalnoj grafici jest stvaranje terena, posebice planina. Planina se tvori tako da se horizontalno položenom trokutu svaki vrh povisi ili snizi za slučajno odabranu vrijednost. Tako dobivenom trokutu spoje se polovišta stranica te se tako dobivaju četiri nova trokuta. Srednjemu od njih (omeđen trima dužinama koje spajaju polovišta stranica prvotnog trokuta) povisimo ili snizimo vrhove kao i početnom trokutu, ali koristimo dvostruko manje vrijednosti. Postupak sada ponovimo za sva četiri trokuta. Planine se mogu napraviti i na drugi način, pomoću Perlinovog šuma.

Pomoću sustava iteriranih funkcija u tri dimenzije moguće je kreirati raznoliko raslinje – grmove, drveće, busene trave i sl. Ako isto napravimo u trodimenzionalnom sustavu te na kraj svake "grančice" dodamo list, rezultati mogu biti zapanjujuće slični stvarnim pojavama u prirodi.
Nadalje, fraktali se koriste i u kompresiji podataka. Od manje važnih primjena tu je (naravno, vrlo ograničeno) predviđanje nekih stohastičkih procesa kao što su potresi; slaganje snopova optičkih vlakana, oponašanje rada neuronskih mreža za razvoj umjetne inteligencije itd. Za male uređaje kao što su mobiteli proizvode se antene u obliku fraktala koje zbog toga mogu koristiti širok spektar frekvencija ne zauzimajući mnogo mjesta. Uzorak za vojnu kamuflažnu odjeću koristi fraktalnu strukturu koja se nigdje ne ponavlja te se stoga mnogo teže zamjećuje u prirodi, gdje ništa nije matematički pravilno. Provode se istraživanja za liječenje aritmije srca, gdje srce kuca u kaotičnom režimu. Vanjskom stimulacijom srca pokušava se postići prijelaz u pravilan režim. Naposlijetku, neke su fraktalne strukture izrazito lijepe te se prezentiraju kao umjetnička djela.
Fraktali u prirodi[uredi | uredi kod]


Mogućnost primjene fraktala leži u činjenici da mnogi od njih sliče prirodnim pojavama. Često se kao primjer spominje posebna vrsta brokule te paprat. Med kristalizira u fraktalne oblike, a drveće je, kao i paprat, po svojoj prirodi fraktalnih svojstava (deblo se grana na grane koje se granaju na grančice...). Zapravo, na neki je način gotovo cijeli svijet sačinjen od fraktalnih oblika. Mandelbrot je koristio primjer obale mora kao fraktal – uvale sliče zaljevima, rtovi poluotocima... Kad bismo se malo približili, svaka bi stijena sličila poluotoku. Veće približavanje otkriva izbočine u stijeni koje također podsjećaju na poluotoke. U tim izbočinama postoje sitne udubine koje imaju isti oblik kao i zaljevi. Takav se postupak može nastaviti sve do molekulskih razmjera. Mnogo je dijelova ljudskog tijela fraktalne strukture. Očit je primjer sustav krvnih žila, koje u principu imaju istu strukturu kao i drveće. DNA se namata dajući fraktalnu strukturu... Primjeri su nebrojeni.
Vidi još[uredi | uredi kod]
- Teorija kaosa
- Topološka dimenzija
- Fraktalna dimenzija
- Sustavi iteriranih funkcija (IFS)
- Lindenmayerov sustav
Literatura[uredi | uredi kod]
- Barnsley, Michael F.; and Rising, Hawley; Fractals Everywhere. Boston: Academic Press Professional, 1993. ISBN 0-12-079061-0
- Duarte, German A.; Fractal Narrative. About the Relationship Between Geometries and Technology and Its Impact on Narrative Spaces. Bielefeld: Transcript, 2014. ISBN 978-3-8376-2829-6
- Falconer, Kenneth; Techniques in Fractal Geometry. John Wiley and Sons, 1997. ISBN 0-471-92287-0
- Jürgens, Hartmut; Peitgen, Heins-Otto; and Saupe, Dietmar; Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992. ISBN 0-387-97903-4
- Mandelbrot, Benoit B., The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982. ISBN 0-7167-1186-9
- Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; The Science of Fractal Images. New York: Springer-Verlag, 1988. ISBN 0-387-96608-0
- Pickover, Clifford A., ed.; Chaos and Fractals: A Computer Graphical Journey - A 10 Year Compilation of Advanced Research. Elsevier, 1998. ISBN 0-444-50002-2
- Jones, Jesse, Fractals for the Macintosh, Waite Group Press, Corte Madera, CA, 1993. ISBN 1-878739-46-8.
- Lauwerier, Hans, Fractals: Endlessly Repeated Geometrical Figures, Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. ISBN 0-691-08551-X, cloth. ISBN 0-691-02445-6 paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
- Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850839-7.
- Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric; Exploring Fractals on the Macintosh, Addison Wesley, 1995. ISBN 0-201-62630-6
- Lesmoir-Gordon, Nigel; "The Colours of Infinity: The Beauty, The Power and the Sense of Fractals." ISBN 1-904555-05-5
- Liu, Huajie; Fractal Art, Changsha: Hunan Science and Technology Press, 1997, ISBN 9787535722348.
- Gouyet, Jean-François; Physics and Fractal Structures (Foreword by B. Mandelbrot); Masson, 1996. ISBN 2-225-85130-1, and New York: Springer-Verlag, 1996. ISBN 978-0-387-94153-0. Out-of-print. Available in PDF version at.„Physics and Fractal Structures” (fr). Jfgouyet.fr. Pristupljeno 2010-10-17.
- Bunde, Armin; Havlin, Shlomo (1996). Fractals and Disordered Systems. Springer. Arhivirano iz originala na datum 2020-10-14. Pristupljeno 2014-10-03.
- Bunde, Armin; Havlin, Shlomo (1995). Fractals in Science. Springer. Arhivirano iz originala na datum 2020-10-01. Pristupljeno 2014-10-03.
- ben-Avraham, Daniel; Havlin, Shlomo (2000). Diffusion and Reactions in Fractals and Disordered Systems. Cambridge University Press. Arhivirano iz originala na datum 2011-10-04. Pristupljeno 2014-10-03.
- Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press.
Vanjske veze[uredi | uredi kod]
- sistematizirana predavanja o fraktalima sa sveučilišta u Yaleu Arhivirano 2007-10-07 na Wayback Machine-u (en)
- e-škola - jednostavno objašnjeno Arhivirano 2008-10-28 na Wayback Machine-u (sh)
- Fraktalni oblici u numeričkim aproksimacijama (sh)
- Chaos and fractals (en)
- svojstva fraktala Arhivirano 2006-09-01 na Wayback Machine-u (en)
