Mandelbrotov skup

Mandelbrotov skup

Mandelbrotov skup je skup točaka c kompleksne ravnine za koje je Julijin skup (u užem smislu) povezan. Dobio je ime po francusko-američkom matematičaru Benoîtu Mandelbrotu.

Konstrukcija

Preko slike Mandelbrotovog skupa nacrtani su mali Julijini skupovi čija vrijednost c odgovara koordinati kompleksne ravnine na kojoj se nalazi središte svakog od njih.

U Julijin skup (u užem smislu), kao što je već rečeno, može se uvrstiti bilo koji kompleksni broj c. Ovisno o tom broju, Julijin skup može biti povezan ili nepovezan. Ako na kompleksnoj ravnini označimo sve brojeve c pomoću kojih se dobiva povezan Julijin skup, definirali smo Mandelbrotov skup. Mandelbrotov se skup može prikazati na isti način na koji se najčešće prikazuje Julijin skup – bojeći točke koje pripadaju skupu crno, a ostale u raznim nijansama ovisno o tome koliko brzo divergiraju.

Svojstva

Osnovna

Mandelbrotov skup (crno) u kompleksnoj ravnini

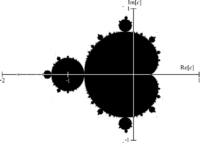
Mandelbrotov je skup zatvoren skup kojemu su sve točke unutar (zatvorenog) kruga polumjera 2 sa središtem u ishodištu. Štoviše, točka c pripada Mandelbrotovom skupu ako i samo ako vrijedi $|f_{c}^{n}(0)|\leq 2$ za sve $n\geq 0$. Drugim riječima, ako je apsolutna vrijednost $f_{c}^{n}(0)$ za neki $n\geq 0$ veća od 2, niz će težiti u beskonačnost (divergirati). Presjek Mandelbrotovog skupa s realnom osi daje interval [−2, 0.25]. Površina se procjenjuje na 1.506 591 77 ± 0.000 000 08, te se vjeruje da je jednako ${\sqrt {6\pi -1}}-e=1.506591651\ldots$

Samosličnost

Mandelbrotov je skup kvazi samosličan (vidi Podjela fraktala) jer se u njemu pojavljuju izmijenjene verzije njega samog. Izmijenjene su uglavnom zbog skupova točaka koji "vire" iz njih povezujući ih s glavnim dijelom (dio 1 u podnaslovu ispod, slika desno).

Atraktori perioda-n

Skupovi točaka konvergiraju onom broju vrijednosti kojim su označene.

Zanimljivo je da u području označenu brojkom 1 na slici sa strane svaka točka konvergira samo jednoj vrijednosti (ne nužno istoj za svaku točku), odnosno tijekom iteracija stvara atraktor perioda-1 (vidi Bifurkacijski dijagram populacijske jednadžbe). Na području 2 svaka točka čini atraktor perioda-2. U Mandelbrotovom skupu postoji barem jedno područje za atraktor perioda-n, $n\in \mathbb {N}$. Područja koja su izravno spojena s područjem 1 tvore atraktor perioda-n ako iz njih "viri" n-1 "antena":

Galerija uvećavanja

Svaka slika predstavlja jedan uvećani dio prethodne. Vidljiva je beskonačna složenost skupa i bogatstvo geometrijskih struktura. Uvećanje zadnje slike u odnosu na prvu je otprilije 60 000 000 000 : 1. Na prosječnom monitoru zadnja slika bi bila dio Mandelbrotovog skupa promjera oko 20 milijuna kilometara.

	I	II	III	IV
V	VI	VII	VIII	IX
X	XI	XII	XII	XIV

Varijacije

multibrot skupovi trećeg i četvrtog stupnja

Moguće je napraviti Mandelbrotov skup pomoću funkcije $f(z_{n-1})=z_{n}^{b}+c,b>2$. Takvi se skupovi popularno nazivaju multibrot skupovima.

Vanjske veze

• "Mandelbrot set - The most advanced online generator"

Vidi još

Mandelbrotov skup na Wikimedijinoj ostavi

• Fraktali
• Julijin skup
• Gorući brod (fraktal)