Kvadratura kruga

Kvadratura kruga je pojam vezan za najpoznatiji antički matematički problem. To je skraćeni naziv za problem koji se najčešće opisuje rečenicom:
Sam naziv je opis matematičkog postupka konstrukcije kvadrata iste površine kao i krug. Bitno je naglasiti da su Heleni preferirali konstrukciju, a ne numeričko izračunavanje.
Pošto je površina kvadrata , a površina kruga tada iz jednakosti površina proizilazi da je . Još su Heleni umeli da geometrijski pomnože dva broja, tj dve duži, odnosno da geometrijski nađu kvadratni koren broja, ali je za rešavanje ovog problema potrebno geometrijski konstruisati broj π. Geometrijska konstrukcija broja π je nemoguća, a to je tek 1882. godine pokazao Lindeman dokazujući da π nije algebarski već transcendentan broj.
Izraz kvadratura kruga u svakodnevnom životu metafora i označava nerešiv problem, mada je neki koriste za opis beznadežnog ili besmislenog. Pretpostavlja se da je na ovaj problem tokom ljudske istorije potrošeno više intelektualnog napora nego za slanje čoveka na Mesec.
U stvari, postoje egzaktna rešenja, ali ako se ne poštuju pravila konstrukcije lenjirom i šestarom. Lenjirom i šestarom je moguće uraditi približnu konstrukciju, sa izvesnim stepenom aproksimacije.
Ovo važi za euklidsku geometriju, u neeuklidskoj geometriji je formula za površinu kruga drugačija pa je i kvadratura kruga moguća u nekim slučajevima.
Ne treba poistovećivati ovaj problem sa problemom kvadrature kruga Tarskog.
Drevne kvadrature[uredi | uredi kod]
Prvi pokušaj kvadrature kruga možemo naći još kod Starih Egipćana u Ahmesovom papirusu, oko 1650. g pne. Ahmes piše da treba konstruisati kvadrat od 8/9 prečnika kruga.
Heleni su prvi definisali ovaj problem na precizan način. Priznavali su rešenje koje poštuje pravila konstrukcije lenjirom i šestarom. Prvi Helen koji se bavio kvadraturom kruga je Anaksagora, doduše u zatvoru, kao bogohulni filozof.
Sledeći kvadraturaši (grč. τετραγωσιειν) Antifon i Brison razmatraju kvadraturu ali njihovi spisi su izgubljeni. Mnogi Heleni posle njih pokušavaju, ali ne uspevaju. Oni su makar bili izuzetno pošteni i profesionalni i nisu podvaljivali i varali u tvrdnji da su uspeli.
Arhimed nije rešio kvadraturu, ali je prvi utvrdio da je površina kruga jednaka površini pravouglog trougla čija je jedna kateta jednaka poluprečniku a druga obimu kruga. Prikazao je osobine spirale kojom se može izvršiti kvadratura, ali je to rešenje ubrojano u mehanička.
Od 1050. g, kada je Franko od Liža objavio knjigu De quadratura circuli gde navodi konstrukciju kvadrature u kojoj je π=22/7, do današnjih dana broj ljudi koji su jurili slavu objavljujući da su konačno rešili najteži matematički problem svih vremena je ogroman. Pariska Akademija 1775. godine objavljuje da prestaje da prima i razmatra prijave u vezi kvadrature kruga. Broj prevaranata amatera i dalje nastavlja da raste, pa je za ovu oblast dat naziv pseudomatematika.
Geometrijska kvadratura[uredi | uredi kod]
Heleni nisu numerički nego geometrijski rešavali problem. Bili su izuzetno vešti i mudri. Kada se problem nije uspeo savladati šestarom i lenjirom, pronašli su izvesne krive, zanimljivih osobina, koje su se mogle koristiti za rešenje raznih problema pa i kvadraturu kruga. Sigurno znamo za sledeće krive:

Hipiasova kvadratrisa[uredi | uredi kod]
Pronalazak ove krive se pripisuje Hipiasu, ali se prva uspešna demonstracija na konstrukciju kvadrature kruga pripisuje Dinostratusu.
Postupak kvadrature: Konstruiše se jedinični krug i opiše kvadrat oko njega. Konstruiše se kvadratrisa. Izračuna se recipročna vrednost od AG=2/π i pomnoži sa 2 što je AL=π. Opiše se krug da bi se izračunao koren iz π. Sa tom stranicom se konačno konstruiše kvadrat jednak krugu, što je i trebalo pokazati.
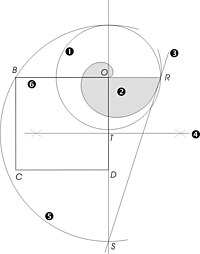
Arhimedova spirala[uredi | uredi kod]
Prvi je otkrio Konon, ali je Arhimed opisao brojne osobine i, među njima, primena na problem kvadrature kruga.
Postupak kvadrature: Konstruiše se jedinični krug i u njemu spirala koja čini jedan pun obrt pre nego što preseče krug. Iz tačke preseka se povuče tangenta na spiralu. Povuče se normala na poluprečnik u tački preseka i dobije se tačka S. Sada je OS=π. Opiše se krug TS da bi se izračunao koren iz π. Sa tom stranicom se konstruiše kvadrat jednake površine kao i krug, što je i trebalo pokazati.
Međutim ove metode su proglašavane mehaničkim, jer su za crtanje tih krivih linija morale biti konstruisane posebne mehaničke naprave, pošto lenjir i šestar nisu bili dovoljni.
Numerička kvadratura[uredi | uredi kod]
Ovo je metoda u kojoj se π aproksimira nekim razlomkom ili algebarskom vrednošću do neke željene tačnosti pa se pristupa konstrukciji takvog broja.
- Među najbolje aproksimacije spada jedna stara od poljskog jezuitskog sveštenika Kočanskog oko 1685. godine (konstrukcija)
- Ramanudžan (1913.) i Olds (1963.) su opisali konstrukciju za .
- Dikson (1991.) je dao konstrukciju u kojoj je
, gde je φ zlatni presek i
.
Moderne prevare, prevaranti i druge besmislice[uredi | uredi kod]
Tokom 20. veka je rekord najviše izdatih tekstova o kvadraturi kruga držao izvesni Džejms Smit. Za njega važi da nije na osnovu dobrih pretpostavki izvlačio pogrešne zaključke već da njegovi zaključci nemaju veze sa pretpostavkama. Njegova upornost da dokaže da je π=25/8 je rezultovala brojnim knjigama na tu temu.
De Morgan je 1872. godine predložio da svetac zaštitnik kvadraturaša kruga bude Sveti Vito. Postoji ples posvećen ovom svecu u kome učesnici vrište i urlaju, vrteći se u krug, što vodi do masovne histerije. Takođe je predložio da lekari prihvate novu dijagnozu morbus cyclometricus za ljude obuzete kvadraturom kruga.
Skupština Savezne države Indijane je 5. februara 1897. godine predložila zakon kojim se proglašava zvanična vrednost broja π koja se ima upotrebljavati u državi Indijani. Izvesni Edvard Gudvin, predlagač, je zakon tako loše napisao da se spominju četiri različite vrednosti za π ali je za svaki slučaj zaštitio svoje otkriće kopirajtom. Autor je velikodušno ponudio državi da koristi njegovu vrednost za π u školskim udžbenicima bez nadoknade dok bi svi ostali plaćali tantijeme. Zakon je prošao donji dom jednoglasno (sa 76:0) ali je zaustavljen u gornjem domu. Niko ne zna da li je zakon ikad skinut sa dnevnog reda ili još čeka na izglasavanje.
Danas više nisu u pitanju samo amateri, već preduzimljive osobe koje svoje pronalaske štite patentima.








