Ciklična grupa
U teoriji grupa, ciklična grupa ili monogena grupa je grupa koja može biti generisana samo od jednog svog elementa, u smislu da je da grupa ima element g ("generator" grupe) takav da, kada se zapiše multiplikativno, svaki element grupe je stepen od g (umnožak od g u slučaju aditivne notacije).
Definicija[uredi | uredi kod]
Grupa G se naziva cikličnom ako postoji element g u G, takav da G = <g> = { gn za svaki ceo broj n }. Kako je svaka grupa generisana elementom grupe podgrupa te grupe, pokazivanjem da je jedina podgrupa grupe G koja sadrži g sama G, pokazuje se da je G ciklična.
Na primer, ako je G = { e, g1, g2, g3, g4, g5 }, onda je G ciklična, i G je u suštini ista kao (do na izomorfizam) grupa { 0, 1, 2, 3, 4, 5 } sa sabiranjem po modulu 6. To jest 1 + 2 mod 6 = 3, 2 + 5 mod 6 = 1, i tako dalje. Može se koristiti izomorfizam φ definisan kao φ(g) = 1.
Za svaki pozitivan ceo broj n postoji tačno jedna ciklična grupa (do na izomorfizam) čiji red je n, i postoji tačno jedna beskonačna ciklična grupa (celi brojevi u odnosu na sabiranje). Stoga su ciklične grupe najjednostavnije grupe.
Ime 'ciklična' može da dovede u zabunu: moguće je generisati beskonačno mnogo elemenata i ne napraviti nijedan ciklus; to jest, svako može biti različito. Grupa generisana na ovaj način je beskonačna ciklična grupa, koja je izomorfna aditivnoj grupi celih brojeva Z.
Grupe se obično označavaju aditivno na sledeći način: Z/n ili Z/nZ. Multiplikativno, označavaju se kao Cn. (Na primer, g3g4 = g2 u C5, gde je 3 + 4 = 2 (mod 5) u Z/5.)
Sve konačne ciklične grupe su periodične grupe.
Svojstva[uredi | uredi kod]
Svaka ciklična grupa je izomorfna grupi { 0, 1, 2, ..., n − 1 } u odnosu na sabiranje po modulu n, ili Z, aditivnoj grupi svih celih brojeva. Zbog toga su ciklična grupe najjednostavnije grupe za izučavanje i imaju brojna zgodna svojstva. data je ciklična grupa G reda n (n može biti beskonačno). Za svako g iz G,
- G je Abelova grupa; to jest, operacija grupe je komutativna: gh = hg. Ovo važi, jer je g + h mod n = h + g mod n.
- Ako je n beskonačno, tada jer n mod n = 0.
- Ako je n = ∞, tada postoje tačno dva generatora: 1 i −1 za Z, a svi ostali se preslikavaju u njih pod izomorfizmom u drugim cikličnim grupama.
- Ako je n konačno, tada postoji tačno φ(n) generatora, gde je φ() Ojlerova fi funkcija
- Svaka podgrupa od G je ciklična. Zaista, svaka konačna podgrupa od G je grupa { 0, 1, 2, 3, ... m − 1} u odnosu na sabiranje po modulu m. A svaka beskonačna podgrupa od G je mZ za neko m, koje je bijektivno (izomorfno) sa Z.
- Cn je izomorfno sa Z/n, jer Z/n = {0 + nZ, 1 + nZ, 2 + nZ, 3 + nZ, 4 + nZ, ..., n − 1 + nZ} { 0, 1, 2, 3, 4, ..., n − 1} u odnosu na sabiranje po modulu n.
Generatori Z/n su klase ostataka celih brojeva koji su uzajamno prosti sa n; broj tih generatora je poznat kao φ(n), gde je φ Ojlerova fi funkcija.
Opštije, ako d deli n, tada je broj elemenata u Z/n, koji su reda d jednak φ(d). Red klase ostatka od m je n / NZD(n,m).
Ako je p prost broj, tada je jedina grupa (do na izomorfizam) sa p elemenata ciklična grupa Cp ili Z/p.
Direktan proizvod dve ciklične grupe Z/n i Z/m je cikličan ako i samo ako su n i m uzajamno prosti. Stoga, na primer Z/12 je direktan proizvod Z/3 i Z/4, ali nije direktan proizvod Z/6 i Z/2.
Definicija implicira da ciklične grupe imaju vrlo jednostavnu prezentaciju grupe Cn = < x | xn >.
Strukturna teorema za konačne Abelove grupe kaže da je svaka konačno generisana Abelova grupa direktan proizvod konačno mnogo cikličnih grupa.
Z/n i Z su takođe komutativni prsteni. Ako je p prost, onda je Z/p konačno polje, što se takođe označava sa Fp ili GF(p). Svako polje sa p elemenata je izomorfno ovom polju.
Jedinice prstena Z/n su brojevi uzajamno prosti sa n. Oni grade grupu u odnosu na množenje po modulu n sa φ(n) elemenata. To se zapisuje kao (Z/n)×. na primer, dobijamo (Z/n)× = {1, 5} kada je n = 6, i (Z/n)× = {1, 3, 5, 7} kada je n = 8.
Poznato je da je (Z/n)× ciklična ako i samo ako je n jednako 2 ili 4 ili pk ili 2 pk za prost broj veći od dva p i k ≥ 1, u kom slučaju se svaki generator Zn× naziva primitivnim korenom po modulu n. Stoga, (Z/n)× je ciklično za n = 6, ali ne za n = 8, kada je izomorfno Klajnovoj četvornoj grupi.
Grupa (Z/p)× je ciklična sa p − 1 elemenata za svako prosto p, što se zapisuje i kao (Z/p)* jer se sastoji od ne-nula elemenata. Opštije, svaka konačna podgrupa multiplikativne grupe bilo kog polja je ciklična.
Primeri[uredi | uredi kod]
U dve i tri dimenzije simetrija grupe za n-puta rotacionu simetriju je Cn, apstraktnog tipa grupe Zn. U tri dimenzije postoje i druge simetrije grupe koje su algebarski iste.
Treba imati u vidu da grupa S1 svih rotacija kruga (kružna grupa) nije ciklična, jer nije ni prebrojiva.
nti De Moavrov broj gradi cikličnu grupu reda n u odnosu na množenje, na primer, gde je i grupa u odnosu na množenje je ciklična.
Predstavljanje[uredi | uredi kod]
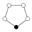
Ciklični grafovi konačnih cikličnih grupa su svi n-tostrani poligoni. Crna tačka u cikličnom grafu predstavlja neutral, a ostali čvorovi su elementi grupe. Cikl se sastoji od uzastopnih stepena bilo kog elementa povezanog sa neutralom.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |