Abelova grupa
Abelova grupa ili komutativna grupa je u matematici grupa (G, * ), gde je je a * b = b * a za svako a i b iz G. Drugim rečima, redosled kojim se binarna operacija sprovodi nije bitan. Ovakve grupe je generalno lakše razumeti, iako su beskonačne Abelove grupe i dalje tema istraživanja.
Grupe koje nisu komutativne se nazivaju ne-Abelove (ili nekomutativne). Abelove grupe su dobile ime po norveškom matematičaru Nilsu Abelu.
Notacija[uredi | uredi kod]
Operacije u Abelovoj grupi mogu biti zapisane aditivno ili multiplikativno.
| Konvencija | Operacija | Neutral | Stepeni | Inverz | Direktna suma/proizvod |
|---|---|---|---|---|---|
| Aditivna | x + y | 0 | nx | −x | G ⊕ H |
| Multiplikativna | x * y ili xy | e ili 1 | xn | x −1 | G × H |
Multiplikativna notacija je uobičajena notacija u teoriji grupa, dok se aditivna notacija obično koristi za module. Kada se Abelove grupe proučavaju odvojeno od drugih grupa, obično se koristi aditivna notacija.
Primeri[uredi | uredi kod]
Svaka ciklična grupa G je Abelova, jer ako su x, y iz G, onda xy = aman = am + n = an + m = anam = yx. Tako, na primer, skup celih brojeva, Z, čini Abelovu grupu u odnosu na sabiranje, kao i celi brojevi po modulu n, Z/nZ.
Svaki prsten je po definiciji Abelova grupa u odnosu na svoju operaciju sabiranja. U komutativnom prstenu invertibilni elementi čine Abelovu multiplikativnu grupu. Skup realnih brojeva je Abelova grupa u odnosu na sabiranje, dok realni brojevi bez nule čine Abelovu grupu u odnosu na množenje.
Matrice formata n × n, čak i invertibilne matrice, ne grade za n > 1 Abelove grupe u odnosu na množenje, jer množenje matrica u opštem nije komutativno.
Tablica množenja[uredi | uredi kod]
Kako bismo proverili da je konačna grupa Abelova, možemo konstruisati tabelu (matricu), poznatu kao Kejlijevu tabelu, sličnu tablici množenja. Ako je grupa G = {g1 = e, g2, ..., gn} pod operacijom ⋅, (i, j)-ti član tabele sadrži proizvod gi ⋅ gj. Grupa je Abelova akko je ova tabela simetrična u odnosu na glavnu dijagonalu (tj. ako je matrica simetrična).
Ovo je tačno, jer je grupa Abelova ako i samo ako je gi ⋅ gj = gj ⋅ gi za sve i, j, dakle da (i, j)-ti član tabele treba biti jednak (j, i)-tom članu.
Svojstva[uredi | uredi kod]
Ako je n prirodan broj i x je element Abelove grupe G zapisane aditivno, onda se nx može definisati kao x + x + ... + x (n sabiraka) i (−n)x = −(nx). Na ovaj način, G postaje modul nad prstenom Z celih brojeva. Zapravo, na ovaj način se moduli nad Z mogu identifikovati sa Abelovim grupama.
Teoreme o Abelovim grupama (tj. modulima nad glavnoidealskim domenom Z) se često mogu uopštiti na teoreme o modulima nad proizvoljnim glavnoidealskim domenom. Tipičan i važan primer je klasifikacija konačno generisanih Abelovih grupa.
Ako f, g : G → H su dva homomorfizma grupa između grupa, pri čemu je H Abelova grupa, tada je njihov zbir f + g, definisan kao (f + g)(x) = f(x) + g(x), takođe homomorfizam. (Ovo nije tačno ako je H ne-Abelova grupa).
Unekoliko srodno dimenziji vektorskih prostora, svaka Abelova grupa ima rang. On se definiše kao kardinalnost najvećeg skupa linearno nezavisnih elemenata grupe. Celi brojevi i racionalni brojevi imaju rang jedan, kao i svaka podgrupa racionalnih brojeva. Dok su netorzione Abelove grupe ranga jedan dobro izučene, čak i Abelove grupe konačnog ranga nisu dobro proučene. Abelove grupe beskonačnog ranga mogu imati veoma složenu strukturu, i još uvek postoji puno otvorenih pitanja, često blisko vezanih za pitanja teorije skupova.
Konačne Abelove grupe[uredi | uredi kod]
Strukturna teorema za konačne Abelove grupe kaže da svaka konačna Abelova grupa može biti izražena kao direktna suma cikličnih podgrupa čiji su redovi stepeni prostih brojeva. Ovo je poseban slučaj strukturne teoreme za konačno generisane Abelove grupe u rangu 0. (Konačno generisane Abelove grupa ranga 0, odnosno čisto torzione, su upravo konačne grupe.)
Na primer, Z/15Z = Z/15 se može izraziti kao direktna suma dve cikličke podgrupe reda 3 i 5: Z/15 = {0, 5, 10} ⊕ {0, 3, 6, 9, 12}. Isto se može reći za svaku Abelovu grupu reda 15, što dovodi do izuzetnog zaključka da su sve Abelove grupe reda 15 izomorfne.
Kao još jedan primer, svaka Abelova grupa reda 8 je izomorfna ili Z/8 (npr. grupa celih brojeva od 0 do 7 u odnosu na sabiranje po modulu 8), Z/4 ⊕ Z/2 (npr. grupa neparnih celih brojeva od 1 do 15 u odnosu na množenje po modulu 16), ili Z/2 ⊕ Z/2 ⊕ Z/2 (npr. grupa uređenih trojki celih brojeva u odnosu na počlano sabiranje po modulu 2).
Zmn je izomorfno direktnom proizvodu Zm i Zn ako i samo ako su m i n uzajamno prosti. Ovde Zn ≅ Z/nZ označava cikličnu grupu reda n.
Prema strukturnoj teoremi i prethodnoj primedbi, bilo koju konačnu Abelovu grupu G možemo da zapišemo kao direktnu sumu oblika
na dva načina:
- gde su brojevi k1,...,ku (redovi podgrupa Gi) stepeni prostih brojeva
- gde k1 deli k2, koje deli k3 i tako dalje do ku.
U svakom od njih brojevi k1,...,ku su jednoznačno određeni (u prvom do na redosled). Koristi se jedan ili drugi zapis već kako je pogodno za dati problem.
Na primer:
- Postoji, do na izomorfizam, tačno jedna Abelova grupa reda 6, naime Z2 ⊕ Z3, odnosno Z6. Slično, svaka Abelova grupa reda 10 je izomorfna Z2 ⊕ Z5, odnosno Z10.
- Abelova grupa reda 12 = 2 · 2 · 3 može biti izomorfna Z4 ⊕ Z3, odnosno Z12, ili može biti izomorfna Z2 ⊕ Z2 ⊕ Z3, odnosno Z2 ⊕ Z6. Pritom ova dva tipa grupe nisu izomorfna među sobom (ovo je iskaz o jednoznačnosti u sturkturnoj teoremi), na primer zato što prva od njih sadrži elemente reda 4, a druga ne.
Automorfizmi konačnih Abelovih grupa[uredi | uredi kod]
Strukturna teorema se može primeniti da se prebroje (i ponekad odrede) automorfizmi date konačne Abelove grupe G. Da bi se ovo uradilo, koristi se činjenica (čiji dokaz ovde neće biti iznet) da, ako je grupa G direktna suma svojih dveju podgrupa H ⊕ K uzajamno prostih redova, tada Aut(H ⊕ K) ≅ Aut(H) ⊕ Aut(K).
Uz ovo, strukturna teorema pokazuje da kako bi se izračunali automorfizmi grupe G, dovoljno je da se izračunaju automorfizmi grupe Silovljevih p-podgrupa odvojeno (to jest, svih cikličnih podgrupa reda stepena p). Fiksirajmo prost broj p i pretpostavimo da su eksponenti ei cikličnih faktora raspoređeni u rastućem redosledu:
- e1 ≤ e2 ≤ … ≤ en
za neko n > 0.
Jedan specijalan slučaj je kada je n = 1, tako da postoji samo jedan ciklični faktor u Silovljevoj p-podgrupi P. U ovom slučaju se može koristiti jednostavna teorija automorfizama konačne ciklične grupe. Naime, automorfizam je jednoznačno određen dejstvom na jedan fiksni generator grupe, koji može preslikati u bilo koji od generatora grupe, i samo njih. Prema tome je u ovom slučaju
- |Aut(P)| = pe − pe−1.
Još jedan specijalan slučaj je kada je n proizvoljno, ali ei = 1 za 1 ≤ i ≤ n. U ovom slučaju, P je izomorfno grupi oblika
- Zp ⊕ … ⊕ Zp,
pa se elementi ove podgrupe mogu posmatrati kao da sačinjavaju vektorski prostor dimenzije n nad konačnim poljem od p elemenata Fp. Automorfizmi ove podgrupe su stoga dati invertibilnim linearnim transformacijama, pa
- Aut(P) ≅ GL(n, Fp),
za šta jednostavan argument brojenjem pokazuje da je reda
- |Aut(P)| = (pn − 1) … (pn − pn−1).
U najopštijem slučaju, gde su ei i n proizvoljni, automorfizam grupe je teže odrediti. Poznato je, međutim, da ako se definiše
- dk = max{r | er = ek}
i
- ck = min{r | er = ek},
tako da posebno imamo dk ≥ k ≥ ck, tada je
Ovo daje redove iz prethodnih primera kao specijalne slučajeve.
Spisak malih Abelovih grupa[uredi | uredi kod]
Sledi tabela malih Abelovih grupa.
Imati u vidu da na primer "3 × Z2" znači da postoje 3 podgrupe tipa Z2, dok na drugim mestima krstić predsatvlja direktan proizvod.
| Red | Grupa | Podgrupe | Svojstva | Ciklični graf |
|---|---|---|---|---|
| 1 | trivijalna grupa = Z1 = S1 = A2 |
- | razna svojstva važe trivijalno | |
| 2 | Z2 = S2 = Dih1 | - | jednostavna, najmanja netrivijalna grupa | |
| 3 | Z3 = A3 | - | jednostavna | |
| 4 | Z4 | Z2 | ||
| Klajnova 4-grupa = Z2 2 = Dih2 | 3 × Z2 | najmanja neciklična grupa | ||
| 5 | Z5 | - | prosta | |
| 6 | Z6 = Z3 × Z2 | Z3, Z2 | ||
| 7 | Z7 | - | prosta | |
| 8 | Z8 | Z4, Z2 | ||
| Z4 ×Z2 | 2 × Z4, Z22, 3 ×Z2 | |||
| Z2 3 | 7 ×
Z22, 7 × Z2 |
ne-neutralni elementi odgovaraju tačkama u Fanoovoj ravni | ||
| 9 | Z9 | Z3 | ||
| Z3 ×
Z3 |
4 × Z3 | |||
| 10 | Z10 = Z5 × Z2 | Z5, Z2 | ||
| 11 | Z11 | - | prosta | |
| 12 | Z12 = Z4 × Z3 | Z6, Z4, Z3, Z2 | 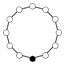 | |
| Z6 × Z2 = Z3 ×
Z2 × Z2 = Z3 × Z22 |
2 × Z6, Z3, 3 × Z2 | 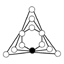 | ||
| 13 | Z13 | - | prosta | 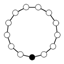 |
| 14 | Z14 = Z7 × Z2 | Z7, Z2 |  | |
| 15 | Z15 = Z5 × Z3 | Z5, Z3 |  | |
| 16 |