Kvadratna jednačina
U matematici, kvadratna jednačina je polinomijalna jednačina drugog stepena. NJen opšti oblik je
gde a ≠ 0. (Za a = 0, jednačina postaje linearna jednačina.)
Slova a, b, i c se nazivaju koeficijentima: kvadratni koeficijent a je koeficijent uz x2, linearni koeficijent b je koeficijent uz x, a c je konstantni koeficijent.

Kvadratna formula[uredi | uredi kod]
Kvadratna jednačina sa realnim (ili kompleksnim) koeficijentima ima dva (ne obavezno različita) rešenja, koja se nazivaju korenima. Rešenja mogu biti realna ili kompleksna, a data su formulom:
gde ± označava da su i
i
rešenja.
Diskriminanta[uredi | uredi kod]

■ <0: x2+1⁄2
■ =0: −4⁄3x2+4⁄3x−1⁄3
■ >0: 3⁄2x2+1⁄2x−4⁄3
U gornjoj formuli, izraz ispod kvadratnog korena:
se naziva diskriminantom kvadratne jednačine.
Kvadratna jednačina sa realnim koeficijentima može imati jedan ili dva različita realna korena, ili dva različita kompleksna korena. U ovom slučaju, diskriminanta određuje broj i prirodu korena. Postoje tri slučaja:
- Ako je diskriminanta pozitivna, postoje dva različita korena, oba realna. Kod kvadratnih jednačina sa celobrojnim koeficijentima, ako je diskriminanta savršen kvadrat, onda su koreni racionalni brojevi, dok u ostalim slučajevima mogu biti iracionalni.
- Ako je diskriminanta jednaka nuli, postoji tačno jedan koren, i taj koren je realan broj. On se nekada naziva dvostrukim korenom, a njegova vrednost je:
- Ako je diskriminanta negativna, nema realnih korena. Umesto njih postoje dva različita (nerealna) kompleksna korena, koji su kompleksni konjugati jedan drugog:
Znači, koreni su različiti ako i samo ako je diskriminanta različita od nule, a realni su ako i samo ako je diskriminanta nenegativna.
Geometrija[uredi | uredi kod]
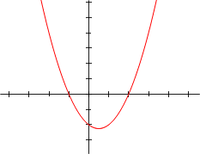
f (x) = x2 − x − 2 = (x + 1)(x − 2) realne promenljive x, the x-koordinate tačaka gde grafik dodiruje x-osu, x = −1 i x = 2, su koreni kvadratne jednačine: x2 − x − 2 = 0.
Koreni kvadratne jednačine
su takođe nule kvadratne funkcije:
jer su to vrednosti x za koje je
Ako su a, b i c realni brojevi, i domen funkcije f je skup realnih brojeva, onda su nule funkcije f tačno x-koordinate tačaka gde grafik funkcije dodiruje x-osu.
Iz ovoga sledi da ako je diskriminanta pozitivna, grafik dodiruje x-osu u dve tačke, ako je diskriminanta jednaka nuli, onda je dodiruje u jednoj tački, a ako je negativna, onda grafik ne dodiruje x-osu.
Kvadratna faktorizacija[uredi | uredi kod]
Vrednost
deli polinom
ako i samo ako je r koren kvadratne jednačine
Iz kvadratne formule sledi da
U posebnom slučaju kada kvadratna jednačina nema dva različita korena (to jest, kada je diskriminanta jednaka nuli), kvadratni polinom se može faktoristi kao
Primena na jednačine višeg reda[uredi | uredi kod]
Određene jednačine višeg reda se mogu lako rešiti pomoću kvadratnih jednačina. Na primer:
se može zapisati kao
gde je
- .
Najveći eksponent mora biti dvostruko veći od eksponenta srednjeg sabirka. Ova jednačina se može rešiti direktno ili korišćenjem jednostavne smene, pomoću metoda za rešavanje kvadratnih jednačina.
Uopšteno govoreći, ako je polinom kvadratni za neku promenljivu u gde je
onda se kvadratna jednačina može koristiti za lakše pronalaženje rešenja.
Istorija[uredi | uredi kod]
Vavilonci su već 1800. pne. umeli da reše par simultanih jednačina oblika:
što je ekvivalentno jednačini:[1]
Početni par jednačina je rešavan na sledeći način:
- oblik
- oblik
- oblik
- oblik
- Zatim se nađe pomoću vrednosti iz (1) i (4).[2]
U spisima Šulba sultras iz stare Indije, oko 8. veka pne., kvadratne jednačine oblika ax2 = c i ax2 + bx = c su ispitivane korišćenjem geometrijskih metoda. Vavilonski matematičari oko 400. pne. i kineski matematičari oko 200. pne. su koristili metod dopune do kvadrata za rešavanje kvadratnih jednačina sa pozitivnim korenima, ali nisu imali opštu formulu. Euklid, grčki matematičar je našao apstraktniji geometrijski metod oko 300. pne.
628. godine, Bramagupta je dao prvo eksplicitno (mada još uvek ne potpuno opšte) rešenje kvadratne jednačine:
| “ | Apsolutnom broju pomnoženim četiri puta [koeficijentom] kvadrata, dodaj kvadrat [koeficijenta] srednjeg člana; kvadratni koren ovoga, manje [koeficijent] srednjeg člana podeljen dvostrukim [koeficijentom] kvadrata je vrednost. (Brahmasphutasiddhanta (Colebrook translation, 1817, page 346)[2] | ” |
Ovo je ekvivalentno sa:
Bakšali rukopis iz Indije, datiran u 7. vek je sadržavao algebarsku formulu za rešavanje kvadratnih jednačina. Muhamed Al Horezmi (Persija, 9. vek) je razvio skup formula koje su radile za pozitivna rešenja. Abraham bar Hija (poznat i pod latinskim imenom Savasorda) je u Evropi uveo kompletno rešenje u svojoj knjizi Liber embadorum iz 12. veka. Baskara II (1114. – 1185.), indijski matematičar i astronom, je dao prvo opšte rešenje kvadratne jednačine sa dva korena.[3]
Spisi kineskog matematičara Jang Huija (1238. - 1298.) su prvi u kojima se pojavljuju kvadratne jednačine sa negativnim koeficijentima od 'x', mada on ovo pripisuje Liu Jiu.
Izvori[uredi | uredi kod]
- ↑ Stillwell, John. 2004. Mathematics and its History. Berlin and New York: Springer-Verlag. 542 pages. p. 86
- ↑ 2,0 2,1 Stillwell, John. 2004. Mathematics and its History. Berlin and New York: Springer-Verlag. 542 pages. p. 87
- ↑ http://www.bbc.co.uk/dna/h2g2/A2982567




























