Wheatstoneov most
Vitstonov most je merni instrument koji je izmislio Samjuel Hanter Kristi 1833, a poboljšao i popularisao Čarls Vitston 1843. Koristi se za merenje električne otpornosti izjednačavanjem dve grane mosta, gde se nepoznata otpornost nalazi u jednoj grani mosta.
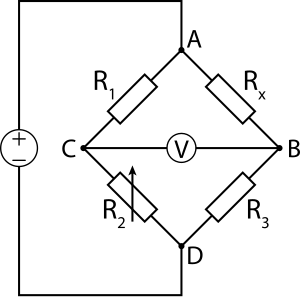
U kolu sa slike, je nepoznata otpornost koja se meri; , i su otpornici poznate otpornosti, a otpornik je promenljiv. Ako je odnos dve otpornosti u poznatoj grani jednak odnosu dve otpornosti u nepoznatoj grani , onda je napon između dva čvora jednak nuli i električna struja neće proticati između čvorova. se menja sve dok se ne postigne ovaj uslov. Smer struje pokazuje da li je preveliko ili premalo.
Detektovanje ravnoteže se može uradili sa izuzetno velikom tačnošću (običnim galvanometrom za jednosmerne struje ili vibracionim galvanometrom za naizmenične struje. Zatim, ako su , i poznati sa velikom preciznošću, onda se i može meriti sa velikom preciznošću. Vrlo male promene u kvare ravnotežu i jasno se otkrivaju.
Ako je most uravnotežen, što znači da je struja kroz galvanometar jednaka nuli, ekvivalenta otpornost kola između izvora napona je:
su paralelno vezane sa
Alternativno, ako su , i poznati, ali nije promenljivo, napon ili struja koje protiču kroz instrument se mogu koristiti da se izračuna vrednost koristeći Kirhofova pravila. Ovakvo podešavanje se često koristi za merenja naprezanja ili temperature putem otpornosti, pošto je obično brža očitati vrednost napona na instrumentu, nego podešavati otpornost do nulte vrednosti napona.
Prvo se Prvim Kirhofovim pravilom da se izračunaju struje u čvorovima B i C:
Zatim se preko Drugog Kirhofovog pravila nađe napon u kolima DBC i BAC:
Most je uravnotežen i , tako da sledi:
Ako se onda jednakosti podele i preurede, dobijamo:
Iz Prvog Kirhofovog pravila vidimo da je i . Vrednost se sada dobija iz:
Vitstonov most ilustruje koncept različitih merenja, koje može biti izuzetno tačno. Varijacije Vitstonovog mosta se mogu koristiti za merenje kapacitivnosti, induktivnosti, impedanse i drugih veličina. Tomsonov most je specijalno prilagođen za merenje vrlo malih otpornosti. Njega je izmislio Vilijam Tomson (lord Kelvin).
Koncept je proširen na merenja naizmeničnih struja od strane Džejmsa Maksvela 1865. i dalje je unapređen od strane Alana Blamlajna oko 1926.





















